【連載:数理生物学の生命観 #5】生命システムの数理 – 現象の背後にある普遍性を目指して

【連載:数理生物学の生命観】
#1 研究者と芸術家の共通点を探る
#2 花をモデルにしたグラフィック作品を制作する芸術家の視点から
#3 生命を扱うアーティストが提示する「感得者を含むモデル」の可能性
#4 現象と数理モデルの双方向性がもたらす美しさ
#5 生命システムの数理 – 現象の背後にある普遍性を目指して
#6 「モデリング」で芸術と科学を再融合する
2019年9月に数理生物学会が開催したシンポジウム「数理生物学の生命観」にご登壇いただいた畠山哲央氏は、生命システムの物理学の構築を試みる研究をいくつも行なっています。
本記事では、現象の背後にある限定的な普遍性に対してアナロジーを慣用し普遍的な性質の展開を試みるという物理的なアプローチを、概日時計とオーバフロー代謝を事例としてご紹介いただきました。普遍性を仮定するという作業は、芸術にも通じるものがあるかもしれません。
なぜ概日リズムはすべての生物において共通の性質を示すのか
これは物理の発想だと思いますが、ある現象があったときに、まずその背後にどういう普遍性があるのかを考えます。この普遍性は必ずしも本当に一般的なものではなくて、ある程度限定されたものかもしれません。そして、アナロジー(類推)を援用しながら、普遍性を利用してモデルを削ぎ落とし、背後にある数理的構造をつかんで、新しい予測を行う。今までそのようにして理論を構築してきました。
まず最初の例として概日時計の話をします。生物はいろいろな種で普遍的に概日時計を持っていることが知られています。バクテリア、カビ、植物、ハエ、人間など様々な生きもので、概日リズムが研究されてきました。概日リズムは日々のサイクルへの適応に重要なのですが、生きものの種類によってまったく異なる遺伝子を使って時計システムを実現しています。少なくとも、4系統の生物種で独立に進化してきたといわれています。
生きものの種類によって使っている遺伝子が違うのに、すべての生物で概日リズムは3つの性質を示すということが知られています。ひとつ目は、一定の環境下において約24時間周期でリズムを刻むこと。2つ目は周期が温度、栄養補償性を示すということ。よく教科書で化学振動の例として出てくるBZ反応(ベロウソフ・ジャボチンスキー反応)の場合、温度を変化させると周期が半分ほどになります。ですが、概日リズムの周期は温度を変えてもほとんど変わりません。それにも関わらず、外から温度サイクルをかけると、概日リズムはすごくきれいに同期することが知られています。この同期できるというのが3つ目の性質です。
つまり、概日時計の周期は温度に対して頑健性(注:変わりにくいこと)を示しながら、一方で位相(注:振動現象において周期の中のある状態の位置。時計でいえば、1つひとつの時刻がひとつの位相に対応する)は温度に対して可塑性(注:変わりやすいこと)を示すわけです。これは時計を作る遺伝子が違っても、普遍的な特徴であることが知られています。これらの性質は一見相反するように思えますが、この2つに何か関係があるのかというのが疑問でした。
そこでまずはシアノバクテリアの概日時計の数理モデルを構築しました。シアノバクテリアの概日時計は非常に面白いシステムです。身の回りにある時計を見てもらいたいのですが、時計は非常に多くの部品からできています。しかし、シアノバクテリアの概日時計は、KaiA、KaiB、KaiCというたった3つのタンパク質とエネルギー源のATP(注:アデノシン3リン酸、細胞内での主要なエネルギー源)を試験管の中に混ぜるだけで、24時間周期の振動を示すという驚きの性質を持っています。このKaiCという一番大きなタンパク質がリン酸化したり、脱リン酸化したりを、24時間周期で繰り返します。
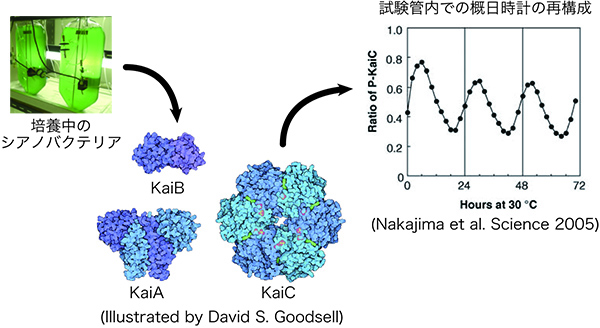
このモデルは、基本的には全部の反応が生化学系のミカエリス・メンテン式で記述されています。このモデルでは、3つのタンパク質は全量試験管の中にあって増えたり減ったりしないので、すべて保存量になっています。そして、KaiCがリン酸化されることで様々な異なる状態をとり、それらが一定の量のKaiAを取り合う形になっています。
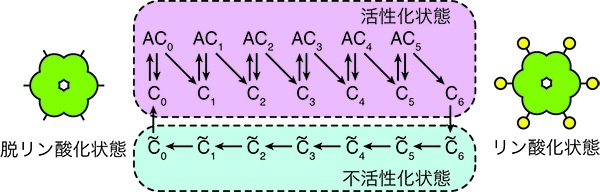
まずは、そもそも温度補償性を示すかどうかが重要です。調べてみたら、このモデルはきちんと温度補償性を示しました。それぞれの化学反応の速度が温度に対して指数関数的に与えられているので、ある程度高温だと周期は温度に対して指数関数的に振る舞います。一方で、ある温度以下では周期が温度にほとんど依存しないということがわかりました。つまり、温度が低い領域で、このモデルは温度補償性を示します。
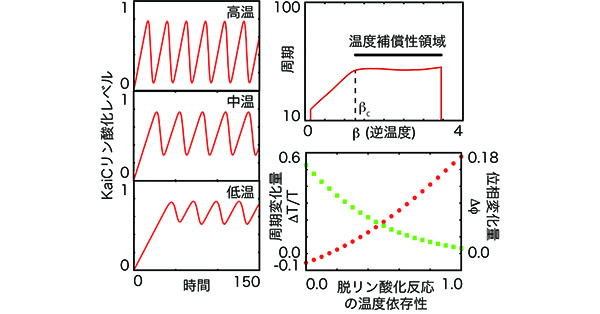
温度補償性が起こる理由の直感的な説明ですが、低温になるとリン酸化の回路を回っているKaiCの実効的な量が低下して、KaiCによるKaiAの取り合いが弱くなります。すると、KaiCと結合していないフリーのKaiAが増えます。そして、その量の変化が反応速度の変化を打ち消すバッファ(緩衝材)として働くことがわかりました。それぞれの反応は温度が低下すると遅くなりますが、フリーのKaiAの量がバッファとして遅くなった反応速度を補償します。
ここで、我々が今一番考えたい問題というのは、温度補償性を示す概日時計が、温度に対する位相の可塑性を同時に示すことができるのはなぜかということでした。重要なのは、この性質が非常に普遍的だということです。
Kaiタンパク質のモデルからわかったことは、生化学反応の速度は温度に依存するが、別の反応がそれを補償するバッファとして働き、それによって温度補償性を示すということです。そこに周期の頑健性の一般的なメカニズムがあるのではないかと考えられます。環境が変化したときに、律速反応の速さは当然変わります。それを打ち消すように、何らかの反応がバッファとして働けば、それで周期の変化を抑えられるのではないか。こういう構造が、Kaiタンパク質のモデルの研究によって見えてきました。
アナロジーを援用しながらと言いましたが、このバッファで速度の変化を打ち消す構造が何かに似てないかと考えたときに、ある入力に対して、Xという要素の変化を、Yという要素を同時に変化させて打ち消すように見えるので、フィードフォワード(注:制御の方法のひとつ。システム生物学の研究において、実際の生物の遺伝子制御ネットワークでフィードフォワードが頻繁に用いられていることが見出された)による適応のネットワークと見なせるわけです。
そこで、周期の頑健性はリミットサイクル(注:巻かれたばねからエネルギーを受け取りリズムを刻むメトロノームのように、外部からエネルギーを受け取って生じる振動のこと。すべての生物リズムはリミットサイクルだと見なせる)うえでの適応現象として捉えられるのではないかという予測をしました。
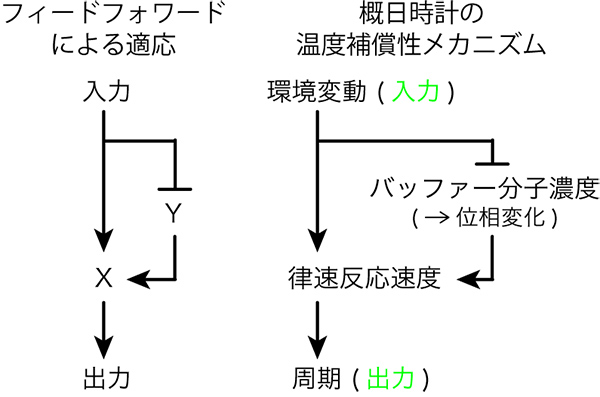
もしこの適応が十分強ければ、周期の変化は小さくなりますが、一方で、過渡的にバッファの量が変わるので、位相が大きく変わります。つまり、適応が十分強ければ、周期の変化は小さくなり、位相の変化が大きくなることが予想されます。一方で、適応が弱ければ、周期の変化が大きくなり、位相の変化が小さくなることが予想されます。つまり、周期の頑健性と位相の可塑性は、普遍的に両立するということが予想されます。
実際に調べてみると、Kaiタンパク質のモデルでは、周期の温度補償性を示す場合、一過的に温度を変化させると、位相がより大きく変わりました。これが実際の生物の中の時計の状態です。一方で、温度変化に対して周期が大きく変わる場合、位相がほとんど変わらないということがわかりました。
ここまではKaiタンパク質の話でしたが、先ほどの仕組みは非常に普遍的に成り立つことが予想されました。そこで、九州大学の巌佐庸さんと理研の黒澤元さんが昔やっていた、ショウジョウバエの概日時計のモデルでも調べてみました。ショウジョウバエの概日時計は、Kaiタンパク質とはまったく違う仕組みで振動を作っているのですが、それにも関わらず見事に周期の頑健性と位相の可塑性の間の関係が成り立ちました。他にもさまざまな時計の例で、この関係は非常に普遍的だということがわかりました。
何かの現象を理解しようとした際に、その中に潜む普遍性を考えて、アナロジーを援用しながら、その本質的な構造を見出すというアプローチは、概日時計の例ではとても有効だったということです。
オーバーフロー代謝とミクロ経済学のアナロジー
2つ目の例はオーバーフロー代謝です。呼吸は非常に効率的にATPを生成できる代謝経路です。しかし、増殖中の細胞では、ATP生成の効率で劣る代謝経路である発酵が、酸素の存在下であっても使用されることが知られています。これがオーバーフロー代謝です。これは大腸菌や酵母、がん細胞などで、普遍的に見られることがわかっています。
このオーバーフロー代謝に対してはいろいろな仮説が提唱されています。たとえば、呼吸がより多くのタンパク質を使うとか、必要なタンパク質を膜に埋め込むために、呼吸はより膜の面積を使用するであるとか、呼吸はATP代謝の効率が良い一方で、NADPH代謝においては発酵がより効率的であるといった仮説です。
ここでの疑問は、多種多様な生物に見られるということは、いろいろな仮説があるが、その根底に何か普遍的な構造があるのではないかということです。そこで代謝をミクロ経済学とのアナロジーを利用して解析することを考えました。
増殖中の細胞では、代謝が進化の過程である程度最適化されているというのが、近年のフラックスバランス解析などでわかっています。実際に、代謝が最適化したとして最適化問題を解くと、代謝状態をある程度きれいに予測できることがわかっています。
一方で、ミクロ経済学では、個人や企業などの経済主体が利益を最適化すると仮定して、その最適化問題を解いています。そこで、代謝の問題を、このフレームワークにうまく乗せられるのではないかと思いました。特に、消費者行動の理論が使えると考えました。
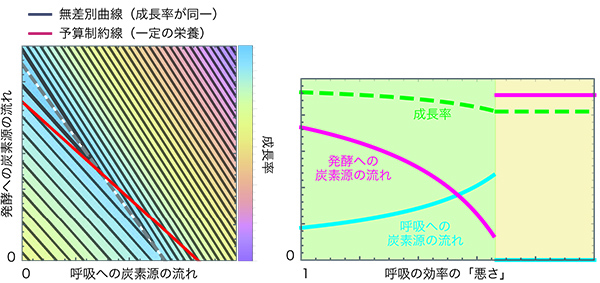
消費者行動の理論というのは、複数の財を一定の収入下で消費するときの、幸福度の最適化問題です。いろいろなものを購入したときにどれぐらい幸福になるかという関数を考えて、収入が一定のときに、どれぐらいの割合で購入するのが一番幸福なのかを考えます。これをオーバーフロー代謝に適用しようと考えました。
ミクロ経済学における各財の需要が、代謝では各代謝経路の流量(フラックス)に対応しています。予算の制約は、栄養の割り振りです。今の場合は、炭素源を呼吸に回すか、発酵に回すかに対応しています。幸福度は成長率に対応します。これから、幸福度の関数を描くことができます。
この対応を利用することによって、過去に提唱されていたいろいろな仮説が、実は同一の最適化問題として表されるということがわかりました。これにより、炭素源が少ないときはATP効率に優れる呼吸だけをして、炭素源が多くなっていくと発酵をするようになることが最適化の結果なのだときちんと示すことができました。がん細胞でも、酵母でも、大腸菌でも、すべて普遍的な構造に支配されているということがわかりました。
また、経済学ではすべての財は、実は3種類に分類されることがわかっています。そのなかにギッフェン財という変わった財があります。これは、値段が上がるとより需要が上がるという財です。普通の財は値段が上がると需要が下がるので、これは変です。驚くべきことに、オーバーフロー代謝における呼吸は、実はギッフェン財に対応しているということがわかりました。そして、ギッフェン財との対応から、新規の現象を予言できました。
アナロジーを介した普遍性への洞察
さて、今日では普遍性というのは主に物理学で使用される言葉ですが、アナロジーを慣用し現象の背後にある普遍的な性質の展開を試みるというアプローチは、物理学に限った話ではないと感じています。生命科学では、実は普遍性というのは中心的なコンセプトであったはずでした。たとえば、ジャック・モノーは”Anything found to be true of E. coli must also be true of Elephants”と言いましたし、1920年代には、オランダの生化学者のアルベルト・クライバーという人が、バイオケミカルユーティリティーというものを提唱しています。実は昔は生命科学において普遍性は中心的なコンセプトだったのではないでしょうか。
美術でも実は同じではないかと思っています。すなわち、美術でも生物の普遍性を暗に仮定してるのではないかということです。たとえば、特定の種の生物に生命を代表させるような作品は多いのではないかと思います。あるいは、観客に生命をテーマにした作品を提示している段階で、観客との間に成立する生命観の普遍性を、暗に仮定している場合が多いと思います。
では、アプローチが仮に近かったとして、美術と科学では何が違うのでしょうか。僕は科学哲学者ではないので、科学とはこういうものだということはできませんが、科学の場合は、科学的な制約があるので、すでにわかっているところから、一度にそれほど遠くに行くことはできません。アナロジーを使えば多少のジャンプはできますが、それでも限定的です。
ただ、美術の場合は、ある意味で科学的な制約がないので、全然違う方向からアナロジーを展開したり、あるいは、科学的な制約に縛られた思考ではまるで思いつかないようなところに手が伸ばせるかもしれません。個人的には、芸術家の方々には、科学者がすでにわかっていることの応用ではなくて、美術の視点から、科学者がまるで思いつかないアナロジーを提示して、人類の生命観を広げるよう作品を作っていただければと思います。
参考文献
- Generic temperature compensation of biological clocks by autonomous regulation of catalyst concentration, TS Hatakeyama and K Kaneko, PNAS, 2012
- Homeostasis of the period of post-translational biochemical oscillators, TS Hatakeyama and K Kaneko, FEBS letters, 2014
- Reciprocity between robustness of period and plasticity of phase in biological clocks, TS Hatakeyama and K Kaneko, Physical Review Letters, 2015
- Microeconomics of metabolism: Overflow metabolism as Giffen behaviour, JF Yamagishi and TS Hatakeyama – bioRxiv, 2020
講演者プロフィール
畠山 哲央
生物のことを理解したくて、学部では工学部で制御工学などを、修士では分子細胞生物学を、博士では理論物理学を学び、現在も主に理論的な側面から生命システムについて研究しています。もっと深く生物について知りたいです。
この記事を書いた人
-
切江志龍
東京大学農学生命科学研究科博士課程在籍。主に植物フェノタイピングと形態モデリングの研究を行っています。生物・生命にまつわる芸術や文化史にも興味を持ち、修士課程からは画家モネの描いたスイレンの園芸史について調査しています。
堀部和也
大阪大学大学院理学研究科博士課程。主に大脳皮質の形づくりについてコンピュータシミュレーションを用いた研究を行っている。仮想生物の進化をコンピュータ上で再現し、生まれてくる新奇な個体の観察が日課。生物・生命の理論モデルからそれらを対象とする芸術にも関心を持ち、ハッカソンで出会ったアーティストと一緒に制作を行っている。
この投稿者の最近の記事
 研究成果2020年10月19日【連載:数理生物学の生命観 #6】「モデリング」で芸術と科学を再融合する
研究成果2020年10月19日【連載:数理生物学の生命観 #6】「モデリング」で芸術と科学を再融合する 研究成果2020年10月19日【連載:数理生物学の生命観 #5】生命システムの数理 – 現象の背後にある普遍性を目指して
研究成果2020年10月19日【連載:数理生物学の生命観 #5】生命システムの数理 – 現象の背後にある普遍性を目指して 研究成果2020年10月19日【連載:数理生物学の生命観 #4】現象と数理モデルの双方向性がもたらす美しさ
研究成果2020年10月19日【連載:数理生物学の生命観 #4】現象と数理モデルの双方向性がもたらす美しさ 研究成果2020年10月19日【連載:数理生物学の生命観 #3】生命を扱うアーティストが提示する「感得者を含むモデル」の可能性
研究成果2020年10月19日【連載:数理生物学の生命観 #3】生命を扱うアーティストが提示する「感得者を含むモデル」の可能性



