物理法則による「できること」の制限

私たちの生活は、車、エアコン、携帯電話など、さまざまな道具によって支えられています。こうした道具の動作はすべて物理現象として理解できます。あまりにも私たちの日常生活に溶け込んでいるので普段は意識しないことですが、電子機器などのスイッチを押して機器を起動させることですら、もとをたどればすべて物理現象です。

こうした事実をふまえて、私たちが「どんな道具を使ってもできないこと」を物理法則に基づいて明らかにするという研究が、古くから数多くおこなわれてきました。たとえば、エンジンで熱を仕事に変換する際、その効率には熱力学第二法則から一定の限界が与えられることが知られています。この限界は、「どんなことをしても」超えられない限界です。たとえ宇宙人が、人間をはるかに超える技術を使って作ったエンジンであっても、熱力学が正しいかぎりはこの限界を超えることはできません。

このように、物理法則は私たちができる操作を制限し、しばしば「どうやっても超えることのできない限界」を与えます。今回我々は、こうした「どうやっても超えることのできない限界」をひとつ見つけました。それは、量子力学の世界で「物体を操作する」際に現れてくる限界です。

量子デバイスの世界 – ナノスケールでの物体操作

近年、ナノスケールで動く精巧なデバイスやマシンの研究が活発に行われています。こうした非常に小さな世界では、物事は、私たちの日常的な直観とは異なる「量子力学」の法則に従います。

たとえば、真ん中に仕切りのある箱にボールを入れた場合、日常の世界では「右にボールが入っている」か「左にボールが入っている」かのどちらか一方だけが実現し、両方が実現するということはあり得ません。また一旦箱にボールを入れてしまえば、どちらの状態であるかはその時点で決まってしまいます。ところが量子力学の世界では、「『ボールが右に入っている状態』と『左に入っている状態』が重ね合わさっている状態」という奇妙な状態が実現可能です。こうした「量子的重ね合わせ状態」と呼ばれる状態では、ボールがどちらに入っているかは観測するまで決まっていない、という非常に直観に反することが起こります。

左右に仕切りのある箱にボールを入れた状況
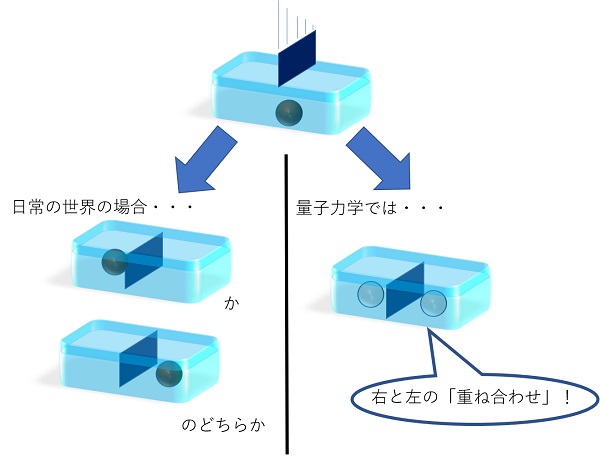
（左）日常的な理解。左右のどちらかにボールが入っていて、それはボールを入れた時点で決まる。
（右）量子力学の場合。左にボールがある状態と右にボールがある状態の重ね合わせ状態となっており、どちらにボールがあるかは箱を開けるまで定まらない。

量子力学の世界はこのように奇妙な性質がありますが、ナノスケールのデバイスやマシンの研究においては、この「量子力学の奇妙な性質」を全面的に利用して、従来の方法で作られた機械をはるかに超える性能を持つ量子機械を作ろうとしています。なかでも有名なものは、量子コンピュータです。現在、古典コンピュータでは素因数分解を素早く解くことができないと考えられていますが、量子コンピュータを使えばこの素因数分解を素早く解くことができます。

こうした量子機械を実現するためには、微小な対象を、量子的重ね合わせを維持したまま高精度で操作・制御する必要があります。これまでは、「そうした操作ができたとして、それを使って何ができるのか？」ということに関しては多くの研究がなされる一方、「どのような装置であれば、そうした操作を行うことができるか？」ということについてはあまり深く考察されていませんでした。しかし、微小な対象を制御することは、それ自体が量子力学的な現象です。したがって、量子の世界で物を操作しようとするとき、そこには量子力学の法則が与える限界が存在しているはずです。

「ゆらぎ」と「精度」のトレードオフ – 量子操作の不確定性関係

今回我々は、操作対象のみならず装置まで含めた全体を量子力学で取り扱い、量子的重ね合わせを維持する操作を高精度で実現させようとする際に、どのような条件を装置が満たさなければいけないのか、ということについて定量的に解析し、ひとつの「どうやっても超えられない限界」を見つけました。

得られた限界は、操作の「誤差」と実験装置の「ゆらぎ」に関するものです。より具体的には、意図していた操作と実際に実現した操作とのあいだの「誤差」の大きさと、操作を実現させる装置における「エネルギーのゆらぎ」の大きさとのあいだに、片方を小さくするともう片方が大きくならなければならないという二律背反な関係（トレードオフ）が存在し、両者を同時に小さくすることはできないということを不等式の形で厳密に証明しました。すなわち、操作を高精度で実現するためには、装置の側のエネルギーが激しくゆらいでいなければなりません。

得られた結果の概念図
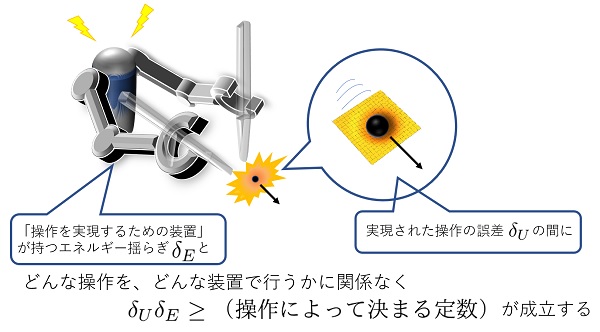
量子的重ね合わせを保つ操作を精度よく行おうとすると、行いたい操作と実際に行われる操作のあいだの誤差\(δ_U\)と、その操作を実現させるための制御装置のエネルギーゆらぎ\(δ_E\)のあいだに、上記の不等式が成立する。この不等式は、「\(δ_U\)と\(δ_E\)のどちらかを小さくしようとすると、それに応じてもう片方が大きくなる」という関係を表している。

得られた不等式は、「もしエネルギーゆらぎの小さな装置を用いた場合には、ある水準以上の精度で意図した操作を実現させることはできない」ことを意味しています。エネルギーゆらぎの小さな装置を用いると、操作対象の量子的重ね合わせを維持するような操作を実現させることができず、対象の量子性が大きく損なわれてしまうのです。こうした量子性の損なわれた操作では、量子デバイスは期待される性能を出すことができません。

この結果は特定のデバイスに関するものではなく、エネルギー保存則をはじめとするいくつかの仮定を満たすすべてのデバイスに適用できるものです。仮定のどれかを破らないかぎり、この不等式が示す限界を超えることはできません。このため、さまざまなデバイスに適用することができます。

量子デバイス設計への応用

今回の結果は、近年盛んに研究されているさまざまな量子デバイスの設計やナノテクノロジーの実現方法を考えるうえで、有益な示唆を与えるものだと考えられます。これまでは、「どのような装置を使えば意図した操作が実現できるか」という問題は個別の事例ごとに考えられており、特定の状況に対してはうまくいく／いかない方法が知られている場合もありましたが、一般的な指針は知られていませんでした。

今回の結果は、極めて一般的な形で高精度の量子操作に対する原理限界を明らかにしており、個別の状況によらない形で操作方法に対する指針を与えることができます。たとえば、もし用いている装置のエネルギーゆらぎがあまり大きくないのであれば、それは量子操作の精度向上を妨げている原因かもしれない、と考えることができます。

今後の展望

今回、我々は量子操作に関する「超えられない限界」を求めました。これは「この条件を装置が満たしていない場合、量子操作は必ず失敗する」という形で与えられています。こうした条件は、必要条件と呼ばれます。ではこの逆、「この条件が成立している装置ならば、量子操作を成功させることができる」という条件はあるでしょうか。これは十分条件と呼ばれるものであり、必要条件の対をなしているものです。現在、我々はこの十分条件を探しています。必要条件と十分条件の対を求め、それらを比較することで、量子操作を行うにはなにをすればよいか、その本質がわかるはずです。

今回の我々の研究結果の詳細を知りたい方は、下記の参考文献をご覧ください。

参考文献
Uncertainty Relations in Implementation of Unitary Operations, Hiroyasu Tajima, Naoto Shiraishi, and Keiji Saito, Phys. Rev. Lett. 121, 110403(2018)

この記事を書いた人

田島 裕康, 白石 直人, 齊藤 圭司
田島 裕康
日本学術振興会特別研究員 (PD)。2015年3月東京大学大学院理学系研究科にて博士号取得。2015年から2018年3月まで理化学研究所　基礎科学特別研究員。2018年4月より現職。物理的な問題と情報理論的な問題のあいだの類似性を使った研究に関心がある。専門は量子情報理論および統計力学。

白石 直人
日本学術振興会特別研究員（PD）。2017年3月東京大学大学院総合文化研究科にて博士号取得。同年4月より現職。テレビ朝日シリーズ「仮面ライダービルド」（2017年9月～2018年8月放送）物理学アドバイザーを務める。過去のインタビュー記事に宇宙でも素粒子でもない物理学-「統計力学」の魅力を慶應大・白石直人研究員に聞く」がある

齊藤 圭司
慶應大学理工学部物理学科教授。専門は統計物理学。