球よりも対称性の高い四面体

数学や物理学、コンピューターシミュレーションなどを駆使することで、実験室で実験を行うことなく、物質の性質を明らかにする学問のことを理論化学と呼びます。実験で得られるデータを正確に解釈したり、新たな化学現象を予測したりするのに用いられます。

最近、我々の研究グループでは、理論化学的手法を用いて特定の金属元素からなる微小な四面体型クラスターが、球対称の原子よりも高い対称性を持つことを明らかにしました。クラスターとは、数個から数十個の原子が集まってできた極小粒子のことです。これらの物質では、その特別な対称性のおかげで既存物質ではありえないほど、多くのエネルギー状態が重なる「超縮退」と呼ばれる現象が起こります。この超縮退を上手く利用すれば、既存物質の限界を超える電気伝導性や磁気特性を生み出すことも可能になると考えられています。

こう聞くと、「あれだけきれいな形をした球よりも対称性が高いってどういうこと？」、「対称性がどうして材料の性質と関係するの？」と疑問に感じる方も多いと思います。本稿ではその秘密に迫るため、「対称性」と「ミクロな物質の世界」の関係について、少し考えてみたいと思います。

対称性ってなに？

対称性は、自然科学の世界で最も重要な概念のひとつです。シンメトリーとも呼ばれ、美しさの尺度とされます。対称性とはなんでしょうか？ それは「ある操作をしても、元のまま変わらない」という性質です。左右対称を思い浮かべるとイメージしやすいかもしれません。ある物体を1枚の平面で切ったとき、左右両側が互いに鏡で映した形になっていれば、左右対称であると言います。ここでの対称性は「鏡に映す操作（すべての点を面対称な位置に移す操作）をしても、元の形にそのまま重なる」ことです。

こういった姿かたちの対称性を幾何学的対称性と呼びます。先ほどの鏡映操作以外にも、反転操作・回転操作・回映操作が幾何学的対称性と関係します。「どれだけの操作に対して、元のままか」を調べることで、さまざまな物体の幾何学的対称性を測ることができます。最も対称性の高い立体は球です。鏡映操作をしようが、回転操作をしようが、球は元のままです。他にも、プラトンの正多面体などが対称性の高い立体として知られています。

物質の対称性とエネルギーの縮退

対称性は、物質の世界で大きな役割を果たします。原子や分子などのミクロな物質が持つさまざまな性質は、それぞれの物質に固有のハミルトニアンと呼ばれる数式とその対称性に依存します。数式の対称性というと不思議に思うかもしれませんが、大事なのは「ある操作をしても変わらない」ことです。先ほど、幾何学的対称性について説明しました。実はこの対称性は、ハミルトニアンの対称性とも密接に関係します。ある幾何学的操作で、ハミルトニアンの持ち主である物質が元のままであれば、ハミルトニアンも変化しません。ハミルトニアンは少なくとも、その物質の幾何学的対称性と同じ対称性を持つのです。

ミクロな物質は、正電荷を持つ原子核と負電荷を持つ電子が集まってできています。各電子は、原子核の周囲に広がる軌道に収容されます。軌道にはさまざまな形があり、おのおのが異なるエネルギーを持ちます。軌道の形やエネルギーの違いが個性となって、その物質の性質が決まります。ハミルトニアンの対称性が高いと、複数の軌道が同じエネルギーを持ちだします。こうしたエネルギー状態の重なりを縮退と呼びます。たとえば、正二十面体状に原子が並んだクラスターでは、幾何学的対称性により、5重に縮退した軌道が現れます。こうした縮退は、特別な電子物性を生み出す原因となることが知られています。

しかし、縮退にも限界があります。分子における最高の幾何学的対称性は正二十面体で、そのときの5重縮退が最大の縮退度です。唯一の例外は原子です。原子の対称性は正二十面体を超えます。原子は、原子核を1個しか持たないため、球対称の物質と見なせるからです。これまでの常識では、原子の持つ対称性や縮退度が「物質が超えることのできない壁」でした。

縮退度の限界を超える

最近、我々はコンピューターシミュレーションによって、マグネシウム、亜鉛、カドミウムなどからなる微小な四面体型クラスターが、6重縮退や10重縮退といった「超縮退」を実現することを明らかにしました。この縮退度は、分子の限界とされる5重縮退だけでなく、球対称の原子すら超えるものです。四面体の幾何学的対称性では本来、3重縮退までしか起こらないはずです。

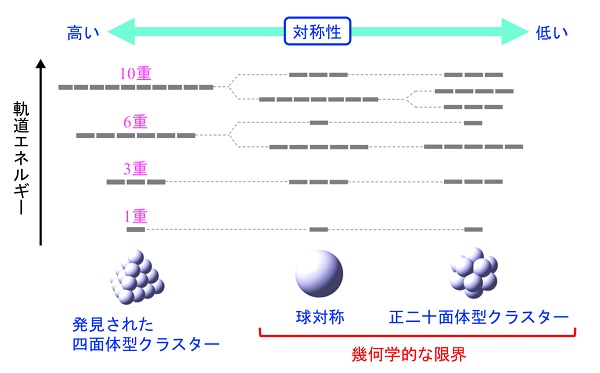
球対称の原子は最も高い幾何学的対称性を持ち、同じエネルギーを持つ状態が最も重なって現れることが知られている。通常、クラスターの対称性は原子の対称性より低いため、原子ほどはエネルギーが重ならない。発見された四面体型クラスターは、特異的な対称性を持つことにより、球対称以上の重なりを示すことが明らかとなった。

超縮退の原因を探ってみましょう。ハミルトニアンは、トランスファー積分を使って書き表せます。トランスファー積分とは、結合で結ばれた原子の間の電子的相互作用の大きさのことで、結合距離に依存するパラメータです。分子に含まれるすべての結合のトランスファー積分を与えてやれば、ハミルトニアンの具体的な形が決まり、軌道やそのエネルギーも求まります。

四面体型クラスターには、幾何学的に等価な結合がいくつか存在します。当然、等価な結合ではトランスファー積分は同じ値をとります。これが幾何学的対称性です。では、互いに非等価な結合のトランスファー積分の比に意味はあるでしょうか？この比を大きくすると、幾何学的対称性を保ちながら、四面体がふくらんでいきます。小さくすると、四面体がへこんでいきます。この比がちょうど\(\sqrt{1}、\sqrt{2} 、\sqrt{3} 、\sqrt{4}\) ……になると、「ややふっくらした構造」で超縮退は起こります。特定の元素でできた四面体型クラスターは、この特殊な条件を満たしていたのです。

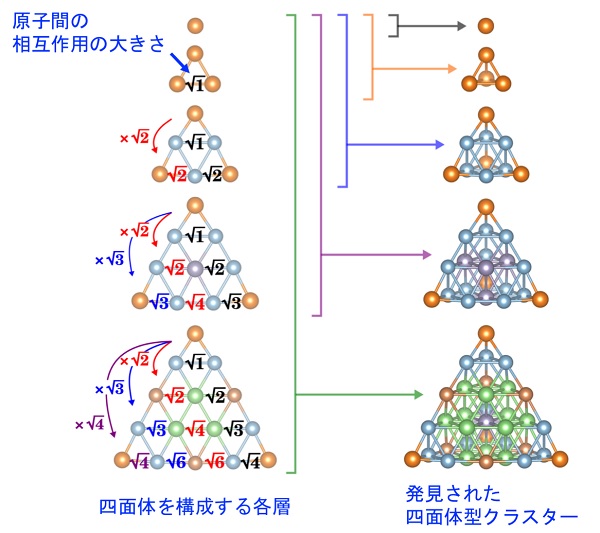
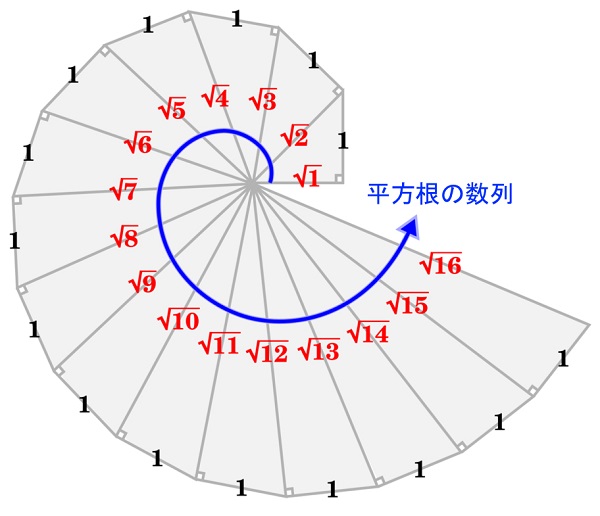
四面体型クラスターにおいて、各原子間の電子的相互作用の大きさ（トランスファー積分）が、図に示した比になるとき、多くのエネルギー状態が重なることがわかった。ここで現れる平方根の数列\(\sqrt{1}、\sqrt{2} 、\sqrt{3} 、\sqrt{4}\) ……は、古代ギリシャのテオドロスによって発見されたものである。

実は、この比の数の並びは、約2500年前に発見された「テオドロスの螺旋」に現れる数列に一致します。古代ギリシャで芽生えた数学が時代を超えて、現代の物質科学で実を結ぶところに限りのないロマンがあります。

テオドロスの螺旋。二辺の長さを1とする直角二等辺三角形の斜辺に、それを底辺とする高さ1の直角三角形をくっつける。さらにその直角三角形の斜辺に、それを底辺とする高さ1の直角三角形をくっつける。これを繰り返すと、大きさの異なる直角三角形がらせん状につながり、各三角形の底辺の長さとして、平方根の数列\(\sqrt{1}、\sqrt{2} 、\sqrt{3} 、\sqrt{4}\) ……が現れる。

超縮退が起こる条件でハミルトニアンを解析してみると、幾何学的対称性とはまったく異なる特別な対称性を持つことがわかります。幾何学的対称性がある場合、いくつかの幾何学的操作に対して、ハミルトニアンの形は変わらないと言いました。実はこのハミルトニアンはそれだけでなく、幾何学的意味を伴わない数学的操作に対しても不変となります。このような非幾何学的対称性を「力学的対称性」と呼びます。今回見つかったクラスターは、球対称以上の力学的対称性によって縮退を起こす世界初のナノ物質だったのです。

超縮退と材料科学の未来

超縮退物質の発見はこれまでにない電子材料や磁性材料の開発につながると期待されています。超縮退した軌道に少しだけキャリア（電流の担い手となる電子、あるいは電子の抜け穴）が混ざれば、高い電気伝導性が引き起こされます。また、超縮退した軌道に電子が1個ずつ並べば、スピン（電子に内在する微小な磁石）が整列し、高い磁性が生み出されます。

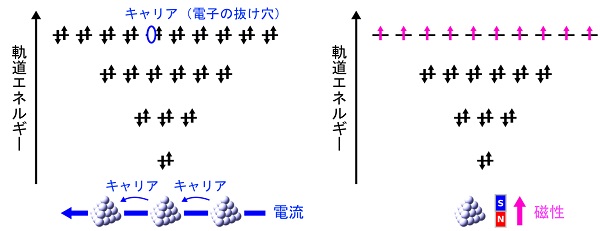
多く重なったエネルギー状態にキャリア（電流の担い手となる電子、あるいは電子の抜け穴）を注入すると電気伝導体になり、スピン（電子に内在する微小な磁石）を整列させると磁性体になる。

こういったキャリア注入やスピン整列は、四面体型クラスターの構成元素を変えたり、合金化したりすることで実現できることがわかっています。今後は、こうしたシミュレーション上のナノ物質の実現に向けたクラスター合成が課題となります。

参考文献
Naoki Haruta, Takamasa Tsukamoto, Akiyoshi Kuzume, Tetsuya Kambe, Kimihisa Yamamoto, “Nanomaterials design for super-degenerate electronic state beyond the limit of geometrical symmetry”, Nature Communications 9, 3758 (2018).

この記事を書いた人

春田直毅
春田直毅
春田 直毅（写真左上）
東京工業大学科学技術創成研究院特任助教。2016年、京都大学大学院工学研究科博士後期課程修了。博士（工学）。東京工業大学科学技術創成研究院研究員を経て、2018年より現職。専門は理論化学、量子化学、振電相互作用、ヤーン・テラー効果、群論の応用。

塚本 孝政（写真右上）
東京工業大学科学技術創成研究院特任助教。2015年、首都大学東京都市環境科学研究科博士後期課程修了。博士（工学）。マイアミ大学化学科訪問研究員、東京大学大学院理学系研究科博士研究員、東京工業大学科学技術創成研究院研究員を経て、2018年より現職。専門は光化学、錯体化学、人工光合成、機能性色素、粘土鉱物、有機－無機複合体、ナノシート、デンドリマー、クラスター化学。

葛目 陽義（写真左下）
東京工業大学科学技術創成研究院特任准教授。2004年、リバプール大学化学科博士課程修了。PhD。リバプール大学化学科博士研究員、アリカンテ大学電気化学研究所博士研究員、慶應義塾大学理工学部助教、東北大学原子分子材料科学高等研究機構助教、ベルン大学化学・生化学科上級博士研究員を経て、2016年より現職。専門は固液界面電気化学、単結晶表面、固液界面（赤外・ラマン）分光学。

神戸 徹也（写真中下）
東京工業大学科学技術創成研究院化学生命科学研究所助教。2014年、東京大学大学院理学系研究科博士後期課程修了。博士（理学）。東京工業大学資源化学研究所産学官連携研究員、東京工業大学資源化学研究所助教を経て、2016年より現職。専門はナノ材料、クラスター、錯体高分子。

山元 公寿（写真右下）
東京工業大学科学技術創成研究院化学生命科学研究所教授。1990年、早稲田大学大学院理工学研究科博士課程修了。工学博士。早稲田大学理工学部助手、早稲田大学理工学総合研究センター助教授、慶應義塾大学理工学部助教授、慶應義塾大学理工学部教授、東京工業大学資源化学研究所教授を経て、2016年より現職。専門は高分子錯体科学、機能材料化学。