なぜ「ファラデーの電磁誘導の法則」は2とおりの方法で導かれるのか?
磁場を時間変化させることで起電力が生まれる「ファラデーの電磁誘導の法則 (Flux Rule)」を覚えていますでしょうか。法則として暗記した記憶のあるかたもいらっしゃるとは思いますが、実はこのFlux Ruleは、古典電磁気学では2つの異なる物理法則から成り立っています。
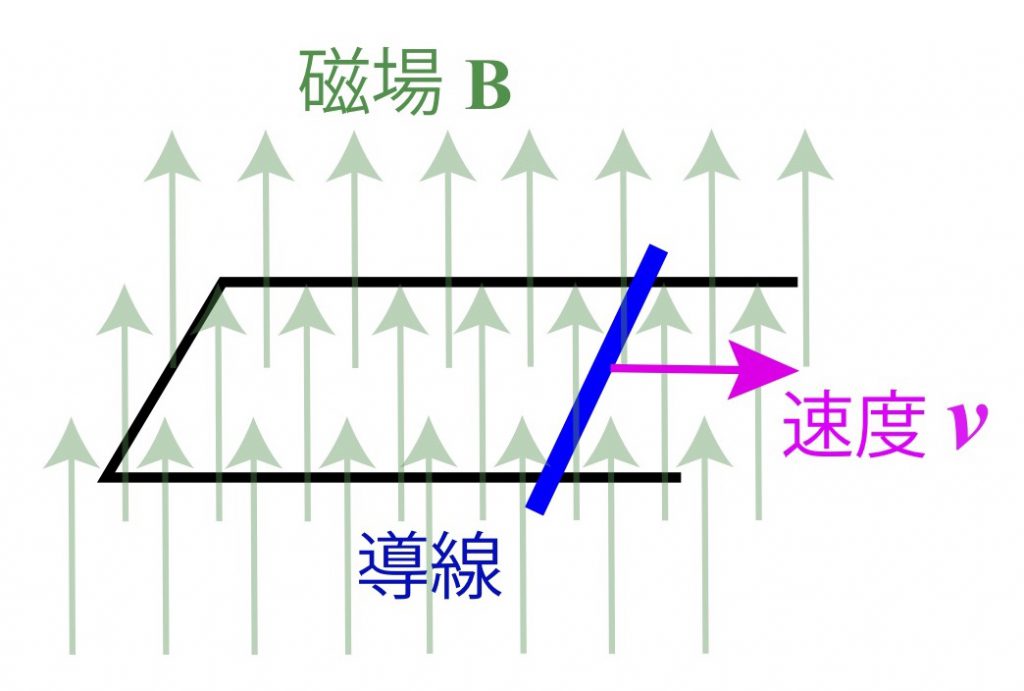
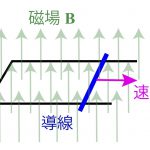
高校物理の教科書には、速度vで動く導線とコの字型の回路に磁場Bが印加されている場合の誘導起電力の計算が記載されており、このとき誘導起電力は、FluxRuleを使った方法とローレンツ力を使った方法の2とおりで導出されています。後者は荷電粒子の存在が必須ですが前者では必要なく、2つの機構における起電力生成は全く別物です。それにも関わらず、両者とも起電力生成は同じFlux Ruleで表されるのです。物理的に全く異なる機構から得られる起電力生成が、Flux Ruleとしてひとつの法則にまとめることができるということは、非常に不思議なことです。
このことに対して、物理学者のファインマンは、
We know of no other place in physics where such a simple and accurate general principle requires for its real understanding an analysis in terms of two different phenomena. Usually such a beautiful generalization is found to stem from a single deep underlying principle. Nevertheless, in this case there does not appear to be any such profound implication. We have to understand the “rule” as the combined effects of two quite separate phenomena”( “The Feynman Lectures on Physics, Vol. II”, 17-1, Addison-Wesley Publishing Company, Reading, Massachusetts, 1964)。(日本語訳:このような 一致が見られるとき、大抵は、統一的な両者を束ねる原理あるものだが、この場合には、それが見当たらない)
と述べています。さらに興味深いことに、アインシュタインの相対論に関する最初の論文にも、磁石と導体がある場合、どちらを動かしても同じ電流が導体に生じるのに、どちらを動かすかで物理の記述が違うことが言及されています。つまり、静止した導体の近くで磁石を動かしたときには、導体に電場に生じ、その電場から力を受けて電子が動き、電流が生成します。これは、レンツの法則に従って生じた電流と考えられます。ところが、静止した磁石の近くで導体を動かした時には、電場は生じませんが、電子に働く起電力がローレンツ力により生じ、電流が発生することになります。
最近私たちは、量子力学とゲージ場としての電磁場を考えることで、これら2つの機構が波動関数のU(1)位相が持つdualityでつながっていることを示しました。つまり、ファインマンが見当たらないと言っていた、“a single deep underlying principle”が見つかったのです。
量子力学では、物理量を表す演算子と物理的状態を表す波動関数の2つで物理を記述します。そして電磁場に対しては、電場や磁場よりも「ゲージポテンシャル」が基本的な物理量として現れます。つまり、電場や磁場はゲージポテンシャルから導かれる2次的なものになります。このときの電場と磁場は、FluxRuleを自動的に満たしますので、ローレンツ力から導かれる誘導起電力をゲージポテンシャルで表すことができれば、奇妙な一致の理由が示せるはずです。
そのとき鍵となるのが、ゲージの自由度とゲージ変換です。ゲージの自由度とは、同じ電場、磁場を与えるゲージポテンシャルはひとつではなく多数あるということです。ここで計算が簡単になるゲージを選べば、物理を損ねることなく運動方程式を計算することができます。量子力学におけるゲージの自由度は、波動関数の変化を伴ったゲージ変換というものになり、荷電粒子の物理的状態を表す波動関数も変換を受けます。
このことはゲージ変換を通じて、電場、磁場、荷電粒子は不可分につながっていることを意味します。古典物理学では電場、磁場は測定しなくても確定値を持って存在することが可能ですが、量子力学では電場、磁場はその観測によって初めて確定値を持つことになります。確定値を持つためには、それらと相互作用する荷電粒子が必要ですので、上記で述べた不可分が現れるのは自然かもしれません。この不可分性により、古典物理学では2つの機構、ひとつは荷電粒子の存在を必要とするもの、もうひとつはしないもので表されるFlux Ruleがつながります。

再び上図の状況を考えてみることにしましょう。x軸方向に伸びた導体棒がy方向に速度vで動いていて、z方向に磁場が印加されています。まず、磁場が存在しない場合を考え、そのときの導体中の電子の波動関数を以下のように表します。
![]()
そして磁場が存在するときに、波動関数を
![]()
と近似してgを求めることにします。eigはU(1)位相因子と呼ばれます。z 軸方向の磁場は、ゲージポテンシャル? = (0, Bx, 0), φ = 0 を使って表します。このときローレンツ力は、波動関数の位相に変化をもたらします。それは、
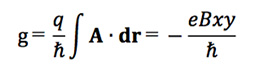
で与えられます。これは、ファインマンの経路積分で磁場からのローレンツ力による位相の変化としてよく知られているものです。q = −eは、電子の電荷です。
導体棒がy軸方向に十分細くy − vt ≈ 0が成り立っているとするとgは−eBvtという運動量を持った並進運動を表す位相となります。これを時間で微分したものがニュートン方程式に現れる力となります。今の場合この力は、−eBvと求まります。これを電荷−eで割って、棒の長さlをかければ起電力Bvlが得られます。つまり、U(1)位相因子eigを全体運動と見たときに、それはローレンツ力で加速する運動となり、誘導起電力が現れます。
次に、U(1)位相因子???をゲージポテンシャルと見ることにします。g ≈ − eBxv/ħt から、ħベクトルポテンシャルのx成分、−???が得られます。これを利用して電場のx成分がBvと求まります。したがって、棒の長さlをかけて起電力はBvlとなります。
上記のように U(1)位相因子eigが全体運動とゲージポテンシャルの2とおりの見方ができるdualityが存在します。そしてそれが、Flux Ruleで表される2つの古典電磁気学的起電力生成機構をつなげます。そこには、量子力学が持つ電場、磁場と荷電粒子の不可分性が垣間見られます。この不可分性は、現在の最先端の理論物理学で現れる「ストリング理論」に通じるものがあります。高等学校で習う内容の奇妙な点が量子力学やストリング理論につながっているということは、大変興味深いことです。
参考文献
H. Koizumi, J. Supercond. Nov. Magn. 30, 3345 (2017).
この記事を書いた人
-
筑波大学計算科学研究センター 准教授。
1985年3月 東京大学教養学部基礎科学科卒業。東京大学大学院物理学専攻博士課程在学中にフルブライト奨学生として米国ノースウェスタン大学留学。1991年9月米国ノースウェスタン大学大学院化学科卒業。PhD。大学院時代は、化学反応の理論的研究を行う。その後、金属クラスター、マンガン酸化物、銅酸化物などの理論的研究を経て、現在は、銅酸化物高温超伝導体の機構解明と、銅酸化物高温超伝導体を利用した量子コンピューター実現に向けた理論的研究を行なっている。趣味は、チェロ(バッハの無伴奏チェロ組曲第6番を挑戦中)と登山。