宇宙空間に広がる素粒子の運動を探る – ブラソフ方程式の高精度シミュレーション
ダークマターやニュートリノの運動
我々の宇宙に存在する銀河や銀河団は、ダークマターを主成分とする物質が宇宙初期のほぼ一様な物質分布から重力相互作用によって形成された天体(自己重力系)であることがほぼ確実となっています。ダークマターは宇宙の質量の大半を占める物質で、光(電磁波)では観測できず、その正体は未だに明らかになっていません。しかし、さまざまな証拠から、何らかの素粒子でできていると考えられています。
ダークマター以外にも、我々の宇宙にはニュートリノという素粒子が多数存在することがわかっています。ニュートリノは、ニュートリノ振動の発見によってわずかながら質量を持つことが明らかとなっているため、銀河の空間分布に見られる宇宙大規模構造の形成に、力学的な影響を与えていると考えられています。
これらダークマターやニュートリノの運動は、粒子の種類や粒子間に働く相互作用の違いに依らず、ブラソフ方程式(無衝突ボルツマン方程式)という共通の方程式を用いて表すことができます。私たちは宇宙空間での粒子の運動を、ブラソフ方程式を使って数値シミュレーションする際の高精度な計算手法を開発しました。
位相空間で物質の運動を眺める
ブラソフ方程式は非常に多数の粒子からなる物質の運動を記述するための方程式です。ある時刻での粒子の運動を特徴づける物理量としては、粒子の位置とともにその速度(運動量)があります。この位置と速度からなる仮想的な空間を位相空間と呼びます。
ある時刻のひとつの粒子の運動は位相空間上の1点で表され、その点は時間の経過とともに位相空間中を連続的に移動します。非常に多数の粒子の運動を扱うには、個々の粒子に対応する位相空間中の多数の“点”の移動を考えるよりも、“点”の数密度を位置と速度の関数として捉え、その時間変化を考えた方が便利です。この“点”の数密度のことを分布関数と呼びます。
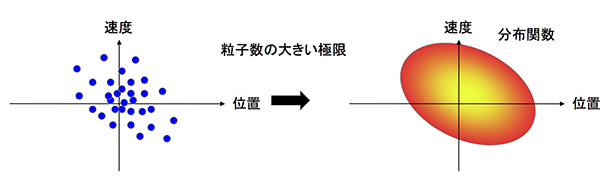
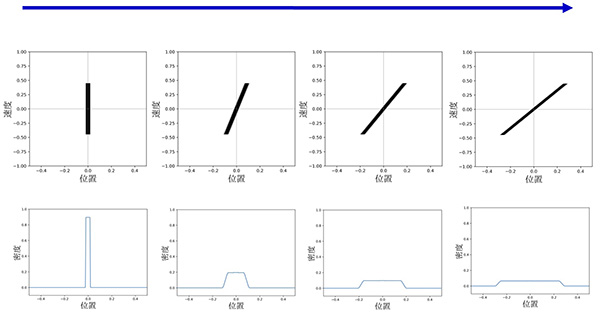
簡単な例として、粒子が1次元的に等速度運動する場合を考えます。位相空間は位置座標と速度座標の2次元空間になり、ある時刻に多数の粒子が原点付近にさまざまな速度を持って存在すると、分布関数は下図上段のようになります。時間が経過すると正の速度を持つ粒子は右に移動し、負の速度を持つ粒子は左に移動します。
上図は粒子が他の粒子や外部から力を受けない場合について述べたものですが、たとえば粒子同士が重力相互作用によって力を及ぼす場合は、重力によって粒子の速度が変化(上下方向に分布関数が移動)し、下図のようなS字型の分布関数に時間発展します。
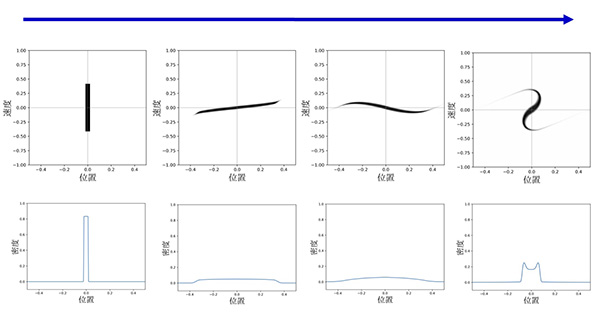
このように時間の経過とともに、位相空間での粒子の分布関数の形が変化します。ブラソフ方程式は、この分布関数が時間とともにどのように変化するかを表す方程式なのです。
6次元の呪い
これまで述べたように、重力相互作用によって天体を形成するダークマターやニュートリノの運動は、ブラソフ方程式で表すことができます。しかしながら、銀河、銀河団、宇宙大規模構造の数値シミュレーションでは、これまでブラソフ方程式が用いられることはほとんどありませんでした。その理由は、3次元空間での数値シミュレーションを実行するには、位置空間の3次元と速度空間の3次元を合わせた6次元という非常に高い次元を持つ位相空間での計算する必要があり、そのためには膨大なメモリが必要なためです。
ブラソフ方程式の数値シミュレーション(以下、ブラソフシミュレーション)では、位相空間を小さな領域(メッシュ)に分割し、ブラソフ方程式を離散化して計算します。同じような計算手法は流体力学シミュレーションでも利用しますが、流体力学方程式の数値シミュレーションは3次元空間を離散化するのに対し、ブラソフ方程式は6次元の位相空間を扱うため必要なメモリが劇的に増加するのです。
粒子シミュレーションからブラソフシミュレーションへ
これまでの研究では、ダークマターやニュートリノの分布を超粒子で表現し、粒子間に働く重力を基に超粒子の運動方程式を解く「粒子シミュレーション」が広く用いられました。
粒子シミュレーションは、位相空間での分布関数を有限個の点でサンプリングして、その点の位相空間での移動を計算するものです。このサンプリング点の個数は本来のダークマターやニュートリノの数と比較すると何十桁も少ないので、粒子シミュレーションでの分布関数は本来の連続的な分布ではなく、超粒子の離散性によるショットノイズが混ざってしまいます。
このノイズは分布関数が大きな領域ではさほど問題にはなりませんが、分布関数が小さい(粒子数密度が低い)領域では状況によって深刻となります。たとえば、宇宙空間を高速で運動するニュートリノは、ダークマターの重力による天体形成を遅らせる無衝突減衰という働きをします。無衝突減衰では、分布関数の値が小さなテイル部分の物質の運動が重要な役割を果たすのです。そのため、この例を粒子シミュレーションで行うと計算結果がノイズに埋もれてしまい、正確なシミュレーションが困難になるのです。
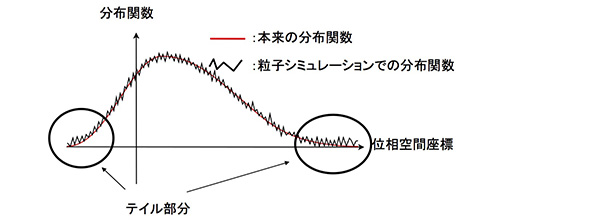
この問題を解決するには、やはりブラソフ方程式を直接数値シミュレーションするのが本質的な解決となります。計算機におけるメモリの大容量化と複数の計算機を束ねて利用する並列計算の技術進歩のおかげで、私たちは世界に先駆けて6次元位相空間での自己重力系のブラソフシミュレーションを実現しました。
高精度数値解法で数値拡散を減らす
ブラソフシミュレーションの最大の困難は、6次元位相空間をメッシュに分割するのに必要なメモリが膨大であることです。もちろん、メッシュの数が多ければ多いほど数値シミュレーションの精度は高くなりますが、ブラソフシミュレーションではただでさえ膨大なメモリが必要なため、これ以上メッシュの数を大幅に増やすのは現実的ではありません。
そこで私たちが取り組んだのが、ブラソフ方程式の数値解法を高精度化するというものでした。一般に、ブラソフ方程式の数値シミュレーションで得られる数値解には、数値拡散という分布関数の輪郭が時間の経過とともにぼやけてしまう性質があります。この性質自体は位相空間を有限個のメッシュに分割して数値シミュレーションする以上避けられないものですが、数値解法を高精度化することによって数値拡散を大幅に減らし、結果として実効的にメッシュ数を増やすのと同じ効果を得ることができます。
ブラソフ方程式には、分布関数の時間や位相空間座標についての微分が含まれています。数値シミュレーションでは、これをメッシュで離散化した分布関数の差分で近似します。この近似の精度を向上させることで、数値拡散を減らすことができます。ただし、一般にこのような高精度化を安易に行うと、分布関数の数値解に非物理的な振動が発生したり、本来は正の値をもつはずが負の値になったりする場合が多々あります。
私たちは、このような非物理的な振る舞いを起こさないことを数学的に保証した、高精度なブラソフ方程式の数値解法を開発しました。数値解法の精度の表し方には次数という指標を使います。同じ大きさの計算領域を分割するメッシュ数を2倍にしたときに数値解の誤差が倍になる精数値解法の精度をN次精度と呼びます。当然、次数の大きな数値解法が優れているわけです。
従来のブラソフシミュレーションでは最高で3次精度の数値解法が用いられていましたが、私たちは5次精度と7次精度の数値解法を開発しました。この5次精度および7次精度の数値解法で得られる結果を自己重力系のブラソフシミュレーションに適用した結果、3次精度の数値解法を用いたものと比較して、はるかに高精度な数値シミュレーションとなっていることを確認しました。
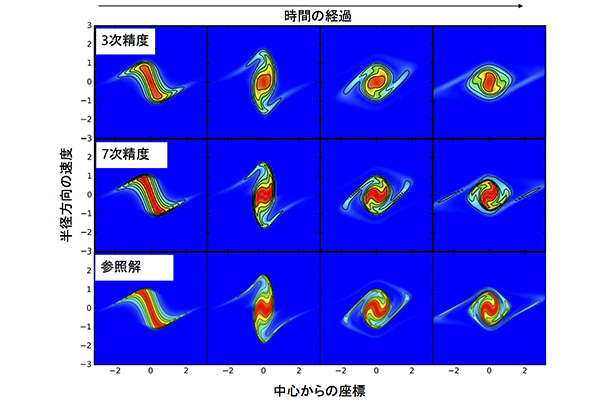
誤差の大きさを比較してみると、7次精度の数値解法を用いた数値シミュレーション結果は、3次精度の数値解法を用いてメッシュ数を8倍にしたものと同等かそれ以上の精度で計算できることがわかりました。
ブラソフシミュレーションが拓く宇宙物理学
私たちが開発した高精度なブラソフ方程式の数値解法の応用として、私たちが考えているのは大きく分けて2つあります。ひとつは、宇宙大規模構造形成におけるニュートリノの力学的影響です。素粒子実験でニュートリノは0でない質量を持つことがわかっていますが、質量の絶対値はいまだにわかっていません。宇宙空間に大量に存在するニュートリノが質量を持つ場合、宇宙大規模構造の形成時に無衝突減衰と呼ばれる、ニュートリノの質量に依存した物理過程が働きます。従って、無衝突減衰の痕跡を宇宙大規模構造の観測でとらえることができれば、ニュートリノ質量の測定につながります。このニュートリノの無衝突減衰の数値シミュレーションは、粒子シミュレーションよりもブラソフシミュレーションの方が適しており、宇宙大規模構造でのニュートリノのダイナミクスをブラソフシミュレーションで調べる研究を現在行っています。
ここでは詳しくは述べませんが、もうひとつの応用としては、宇宙プラズマのダイナミクスがあります。宇宙プラズマの数値シミュレーションについても自己重力系と同様に粒子シミュレーションが使われてきましたが、ブラソフシミュレーションのほうが精度よく計算できる状況がいくつかあります。宇宙プラズマの場合はイオンと電子の分布関数が電磁気力による時間発展をブラソフ方程式で計算します。
ブラソフシミュレーションはこれまでの粒子シミュレーションで扱われてきた自己重力系や宇宙プラズマの研究における新しい研究手段として期待されており、それぞれの分野の研究の進展に大きく貢献すると考えています。
参考文献
Kohji Yoshikawa, Naoki Yoshida, Masayuki Umemura, “Direct Integration of the Collisionless Boltzmann Equation in Six-dimensional Phase Space: Self-gravitating Systems”, 2013, The Astrophysical Journal, 762, 116
この記事を書いた人

-
筑波大学 計算科学研究センター 講師
2002年、京都大学大学院理学研究科 博士後期課程修了。博士(理学)。東京大学大学院理学系研究科ビッグバン宇宙国際研究センター研究員、日本学術振興会特別研究員(PD)、東京大学大学院理学系研究科 産学官連携研究員を経て2007年より現職。専門は宇宙物理学、とくに宇宙大規模構造・銀河団の数値シミュレーションを用いた研究を行っている。




