青銅比準結晶？ – 黄金比でない準結晶を分子シミュレーションで生成

固体には、原子や分子が同じ繰り返し単位で並ぶ「結晶」とランダムに並ぶ「非晶質」しかないと考えられてきましたが、近年さまざまな物質群でそのどちらでもない「準結晶」が発見されるようになってきました。

準結晶は、繰り返し単位のない独特な規則である準周期性と、古典結晶学で許されない正20面体、正12角形、正10角形、正8角形の回転対称性の2つの秩序で特徴付けられていると言われています。また、準周期性は2つ以上の長さスケールに特徴付けられ、それらの比は非結晶学的回転対称性に関連した無理数とされています。

無理数のなかでもとりわけ金属比として知られる黄金比（1.618…）と結びついた10回対称ペンローズタイリングは有名で、その後準結晶の発見に結びつきました。ここでは3番目の金属比である青銅比準結晶タイリングの発見についてご紹介します。

研究の背景

人間が美しいと感じるとされる長方形の比率「金属比」、そのなかでも特に黄金比はギリシャ時代から美術、建築、数学、諸科学で研究されてきました。最近ではダン・ブラウン原作の映画「ダ・ビンチ・コード」で、黄金比とそれに関係したフィボナッチ数が謎解きに使われています。フィボナッチ数と黄金比は自然界や数理科学の所々に現れる不思議な数で、自然界ではパイナップル表面の模様（鱗片）、ひまわりの種、葉序などが知られています。

この黄金比が現代科学に大きな衝撃を与えたのが、一般相対論でも有名な英国オックスフォード大学のペンローズ教授によって発見されたペンローズタイリングです。有名な菱形ペンローズタイリングは黄金比の面積比をもつ2種類の菱形で構成される「非周期的」タイリングで、辺の向きが必ず36度の倍数の向きを向いていること、黄金比の自己相似性があることが特徴です。

1982年4月8日にイスラエルのダニエル・シェヒトマン教授が電子顕微鏡でアルミマンガン合金の観察中に正20面体準結晶を発見し、ペンローズタイリングが物質構造としても存在することが明らかになりました。正20面体のもつ5回回転対称性と周期性がない事実は19世紀末に確立した結晶学の常識を大きく揺るがすもので、2011年シェヒトマン教授にノーベル化学賞が与えられました。このノーベル賞が機会となって準結晶の認知度も上がり、合金系だけでなく液晶、高分子、ナノ粒子など化学分野でも準結晶が次々に発見されています。

一般的に知られているとは言い難いですが、周期性は現在の結晶の定義ではありません。実際、1991年国際結晶学連合（IUCr）は結晶（Crystal）を「Any solid having an essentially discrete diffraction diagram」と再定義し、シャープな回折ピークをもつ準結晶も結晶の一部となっています。従来の結晶は正確に言えば「周期的結晶」とよばれるようになりました。常識というのはたまには疑ってみるものですね。

無理数と準結晶

フィボナッチ数 F_nは 1, 2, 3, 5, 8, 13, 21, 34,…… と成長しますが、数式では

と書かれます。隣り合うフィボナッチ数の比F_n+1/F_nはn→∞の極限をとると、2次方程式

の解である黄金比1.618…に収束することがわかります。つぎに自然数kを使って一般化した

で生成される数列の隣り合う数の比G_n+1/G_nは、同様な2次方程式

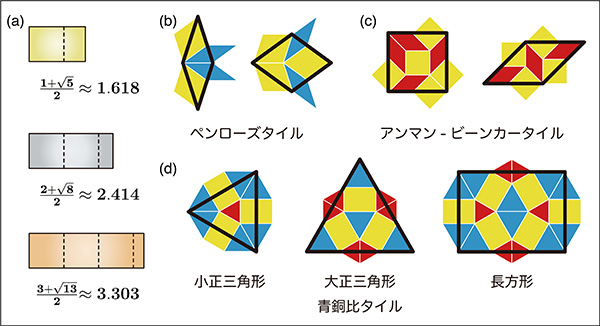
の解に収束します。k = 1 が黄金比、k = 2が白銀比、k = 3は青銅比に対応します（図1(a)）。ちなみにk = 4は黄金比の3乗に対応します。

黄金比は正10角形準結晶（図1(b) ペンローズタイリング）、白銀比は正8角形準結晶（図1(c) アンマン-ビーンカータイリング）、黄金比の3乗は正20面体準結晶のそれぞれの自己相似性に関連していることが知られています。しかし、k = 3の青銅比に関係した準結晶は知られていませんでした。

青銅比を連分数で表記すれば

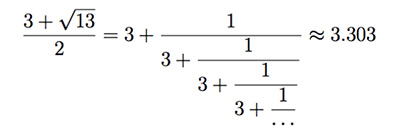
となり、3が無限に続くところが美しいですが、この無理数に関係したタイリングが発見されなかった理由は、この無理数が正多角形からは導かれないことが原因でした。

今回、図1(d)に示す小正三角形、大正三角形、長方形の3種類のタイルを使って青銅比に基づく自己相似な6回の回転対称性を持つタイリングの構成に成功しました。図2のように2種類の長さが交互に現れる12角形を基本として配列することもできます。点線の12角形は色付きタイルの青銅比倍の大きさとなっていることから自分が自分に相似形で隠れているという幾何学的性質である「自己相似性」があることがわかります。

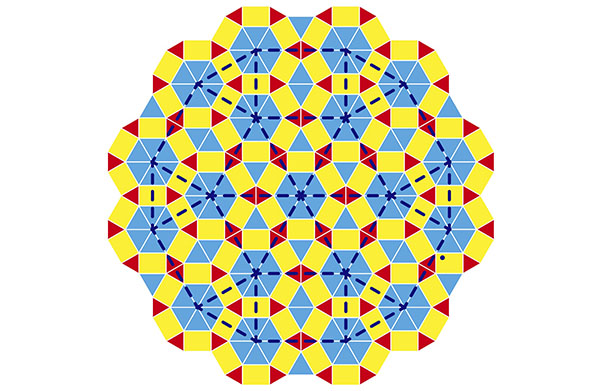
図2を見ればわかるように、一般に「結晶」の証とされてきた6回の回転対称性を持っており、6回の回折図形を持ちます。これまでの準結晶の回転対称性に関する常識「準結晶は非結晶学的回転対称性を持つ」という言い方は必ずしも正確ではないことを指摘しておきましょう。

分子シミュレーションで生成される青銅比準結晶

これまでわれわれは、デンドリマーミセルなどコアシェル粒子系に注目し、2つの長さスケールを持つハードコア矩形ショルダーポテンシャル粒子系の分子シミュレーションで、正3角形と2等辺3角形のモザイクからなる10回、12回、18回、24回対称の回転対称性を持つ2次元準結晶が形成されることを発見してきました。 今回、青銅比準結晶の生成にも成功しました。

図3では、コアシェル粒子そのものが小正三角形、大正三角形、長方形を形成していることを示します。さらに6角形の中心を結ぶと青銅比倍の小正三角形、大正三角形、長方形を形成していることもわかります。この結果は、青銅比準結晶の構成要素がランダムに配列したタイリングが物理的に生じうることを示しています。

まとめ

準結晶の発見によってギリシャ時代から議論されてきた黄金比という無理数と、物質構造にはつながりがあることがわかりました。今回の発見によって、さらに数学と自然に深いつながりが見えてきたように思います。合金系正12角形相の近似結晶や、この1、2年に発表された酸化物準結晶、金属ナノ粒子準結晶にも小正三角形、大正三角形、長方形が現れています。さらに研究が進めば青銅比タイリングの発見が期待できるのではないでしょうか。

参考文献
T. Dotera, S. Bekku & P. Ziherl, “Bronze-mean hexagonal quasicrystal”, nature materials, 16, 987–992 (2017).
T. Dotera, T. Oshiro & P. Ziherl, “Mosaic two-lengthscale quasicrystals”, nature, 506, 208–211 (2014).