量子コンピューターとは、原子や分子、光など、ミクロな世界を記述する量子力学に基づいて動作するコンピューターのことであり、現在我々が使っているコンピューター（古典コンピューターと呼ばれます）をはるかに凌駕する計算能力を持つと期待されています。

量子計算の研究者たちが目指す究極のゴールのひとつは、大量の量子ビットからなるユニバーサル量子コンピューターを作ることです。ユニバーサル量子コンピューターというのは、任意の量子アルゴリズムを走らせることのできる汎用の量子コンピューターのことです。しかしながら、大量の量子ビットを自由自在に操る汎用の量子コンピューターを実験室でつくるのはまだまだ技術的に難しく、実現されていないのが現状です。

そこで、ユニバーサルでなくてもよいから、また、量子ビットの数もそれほど多くなくてもよいから、何か、現在もしくは近い将来の技術のみで実現できるような「弱い」量子コンピューターをまずは作ろう、と考えるのは自然です。実際、GoogleやIBMなどはその方向で研究を進めており、彼らの最近の成果は大きな注目を集めています。

弱い量子コンピューターの代表的な例にone-clean qubit（OCQ）モデルというものがあります。ユニバーサル量子計算を行うためには、まず計算に使うレジスターの状態を全部初期化して「綺麗」にする必要があります。ところが、このOCQモデルでは、レジスターの初期状態は、ノイズののった非常に「汚い」状態であり、たった1個の量子ビットしか綺麗に初期化されていません。このOCQモデルは米国ロスアラモス研究所のKnillとLaflammeにより1998年に提案されたものであり、もともとは、NMR（核磁気共鳴）を使った量子コンピューターの数理モデルとして使われました。NMR量子コンピューターでは偏極率の高い量子ビットを用意するのが難しいため、このような「汚い」レジスターの量子計算として数理的にモデル化したのです（注1）。

このOCQモデルは、量子ビットは実質的には1個しかないわけですから、計算能力はとても弱そうに見えます。それどころか、古典コンピューターでシミュレートできてしまいそうにすら見えます。ところが、驚くことに、このOCQモデルは、古典コンピューターよりは強そうだ、という「証拠」がいくつか見つかってきているのです。たとえば、結び目不変量のJones多項式などいくつかの量を古典計算機よりも高速に計算できることが知られています。

しかしながら、それらの「証拠」は決定的な「証明」ではありません。なぜなら、そこで「古典より高速に計算できる」といっている意味は、「任意の古典アルゴリズムより高速である」という意味ではなく、「現在知られているベストの古典アルゴリズムより高速である」という意味だからです。したがって、明日にでも誰かがそれらの量を高速に計算する古典アルゴリズムを発見してしまうかもしれません。そうなってしまっては、もはや、OCQモデルが古典計算機より高速であるという証拠ではなくなってしまいます。

今回、私は、もしOCQモデルが古典計算機でシミュレートできたら多項式階層が崩壊するという結果を証明しました。

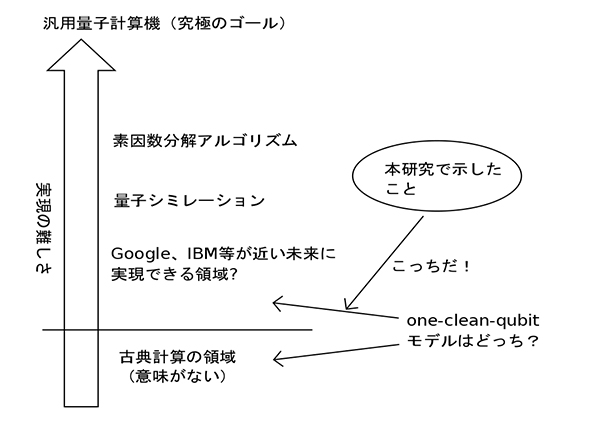
多項式階層というのは、P、NPを一般化した概念であり、崩壊しないだろうと信じられています（不正確ですが、イメージとしてはP=NPが信じられていないようなものです）。したがって、多項式階層が崩壊しないと信じるならば、OCQモデルは古典計算機ではシミュレートできないことになります（注2）。

このように、弱い量子コンピューターが古典計算機より強いことを示す研究は量子スプレマシーと呼ばれており、最近、世界中で流行しています。今回紹介したOCQモデルだけでなく、交換する量子ゲートからなる量子計算モデル（IQPモデル）や、相互作用無しの光子を用いた量子計算モデル（ボソンサンプリングモデル）など、さまざま提案されており、それらの理論的、実験的研究が活発に行われています。近い将来に実現される量子コンピューターはまずはユニバーサルではなく、このような弱いものであるだろうと考えられているため、弱い量子コンピューターは何ができて何ができないのかを明らかにすることが重要となってきています。

量子スプレマシーの研究は量子情報処理という工学的、実用的な話だけでなく、理論物理の基礎とも密接に関係しています。たとえば、量子論の誕生以来、量子と古典の境界がどこにあるのか、という問題は多くの研究者たちの関心を集めてきました。ユニバーサル量子計算機というのはある意味、「最も量子的な存在」なわけですが、それをどんどん弱めていったとき、どこまで弱めたら古典計算機になるのか？ ということが理解できれば、量子と古典の境界がどこにあるのかのひとつの答えとなります。このように、量子計算は、理論物理の基礎に計算機科学の視点からアプローチする、というまったく新しいエキサイティングな研究領域を開拓しているのです！

量子スプレマシーについてもっと詳しく知りたい方は、参考文献をご覧ください。

参考文献
[1] T. Morimae, Hardness of classically sampling one clean qubit model with constant total variation distance error, Physical Review A 96, 040302(R) (2017)
[2]観測に基づく量子計算、7.3節、小柴健史、藤井啓佑、森前智行、コロナ社
[3]量子計算理論、10章、森前智行、森北出版

（注1）あくまで数理的なモデルであり、現実のNMR量子計算機を完全に再現しているわけではありません。
（注2）この結果は、以下で述べる他のモデル（IQPモデル、ボソンサンプリングモデル）の証明と同様に、ある数学的予想の正しさも仮定しています。これは、問題のあるひとつの例を解くのが難しいときに、他の多くの例でも同じように難しいだろう、という予想であり、average case hardness conjectureと呼ばれています。

この記事を書いた人

森前智行
森前智行
群馬大学大学院理工学府　准教授。2009年東京大学大学院総合文化研究科修了。博士（学術）。リール第一大学（フランス）、パリ東大学（フランス）、インペリアルカレッジロンドン（英国）を経て2017年より現職。
ホームページ： http://tomoyukimorimae.web.fc2.com/