小さな物体にはたらく重力の実験で、4次元以上の異次元空間を探す
万有引力の法則は正しくないかもしれない
近代科学の出発点に位置するニュートンの万有引力の法則は、実は小さな距離では正しく成り立つのかどうか、今でも実験でよく確認されていません。特にミクロンスケール以下では重力の存在自身すらも、誰も確認できたことがありません。一方で、その破れは3次元を超える異次元空間、つまり4次元以上の「余剰次元」の空間の存在を示す鍵となる可能性が高く、実験的な検証が注目されています。
私たちは小さな物体間にはたらくきわめて微弱な重力を計測する技術を開発し、余剰次元の探索を大きな目的として重力の精密検証実験を進めてきました。そのなかで、万有引力定数が物質によらない普遍的な定数なのかをミリメートル距離で初めて実験的に確認することに成功しました。
小さな世界でも重力は同じように存在するのだろうか
重力を時空の歪みとして捉える理論であるアインシュタインの一般相対性理論の予言する、重力レンズ効果、重力波、ブラックホールなどの特異な現象は、宇宙物理学的な観測によって次々実証されつつあります。一般相対性理論は太陽系の惑星運動など、低エネルギーではニュートンの万有引力の法則とほとんど同じ予言をし、それらの観測結果はきわめて高い精度で万有引力の法則が正しいことを支持しています。
ところが、ミリメートル以下のようなミクロなスケールに目を向けると、重力の法則は精密に実験・検証が行われておらず、いかなる重力理論も、現在もなお検証が必要な仮説の域を出ていません。これは、重力が電磁気力などの他の力に比べてあまりに弱く、実験的な計測が難しいためです。
4次元以上の空間があるかもしれない
空間は3次元であるという実験的な証拠は数多くありますが、実験で調べられていない小さな4次元以上の空間が存在するはずである、という主張が超弦理論等によりされています。一般相対性理論も万有引力の法則も、空間は3次元であることを前提としているので、もし4次元以上の余剰次元があれば重大な修正が必要になります。
余剰次元はまだ理論的な仮説のひとつに過ぎず、実験的な証拠は何も見つかっていません。また理論的にもそれがあったとしても、何次元あるのか、その大きさは、などはまったくの未知のままです。実験と矛盾しない範囲では、余剰次元は0.1mmのスケール程度まで拡がっていてもおかしくなく、かつ、そこまで拡がると重力が何故弱いのか、という謎を解決できるかもしれないため、その可能性が注目されています。この場合、0.1mm以下では重力の強さが万有引力の法則の予想からずれ始めて、距離が小さくなるほどずっと強くなることが期待されます。これが、私たちが目的として実験を進めている「逆二乗則」の破れの探索です。
逆二乗則とは、距離の二乗に比例して重力が弱まる万有引力の法則の性質のひとつで、空間が3次元であるという仮定から導かれるものです。同様の逆二乗則は電気力なども満たすため、それらの実験から空間は3次元であるとも考えられてきたのですが、余剰次元方向へは電気力は伝搬できないと考えられており、重力だけが余剰次元を観測する手段であると信じられています。余剰次元が存在する場合、余剰次元の拡がりの外側では重力は万有引力の法則に従う一方で、内側では重力は強まり万有引力の法則から逸脱します。そのため、余剰次元の探索をするにはその拡がりの程度まで物体同士を近づけて重力を観測する必要があります。
コロンブスの卵のような画像処理技術で重力を見えるように
万有引力定数を初めて実測して地球の質量を決定したキャベンディッシュは、「ねじれ秤」を用いてそれを成功させました。他に有効な計測方法がないため、この計測方法は現在にいたるまで使われ続けています。
私たちもこの、ねじれ秤を小型化しその動きをビデオカメラで撮影し画像処理解析を施すことで重力を検出します。ねじれ秤とは細いワイヤーに両端に物体をつけた棒をつるした装置であり、この棒にはたらく偶力に応じたねじれ角度を測ることで物体にはたらく力を測定することができます。重力実験においては、ねじれ秤の近くに重力源となる物体を設置することで、重力源からの引力によってねじれを生じさせます。ねじれ秤の動きは画像を目で見てもまったく動きが見られないきわめて微小なものですが、これを捉えるために私たちが開発した画像処理システムを用います。このシステムでは特殊な画像処理を施すことで位置の変化をナノメートルという非常に高い精度で測定することが可能で、私たちのもつ特許技術にもなっています。
センチメートル程度の物体による実験では、重力の強さは地球に対する場合の約1億分の1程度でしかなく、ねじれ秤に現れる変化も微小です。さらに重力に対して、電気力や磁気力、熱や空気の影響が大きいため、近距離での重力の測定をさらに難しくしています。私たちは電気シールドや非磁性の物質の利用、装置内の真空度を上げるなどの工夫をすることで抑制し、また、画像情報を活用することで不必要な振動成分を解析で除去することで重力の検出を可能にしています。
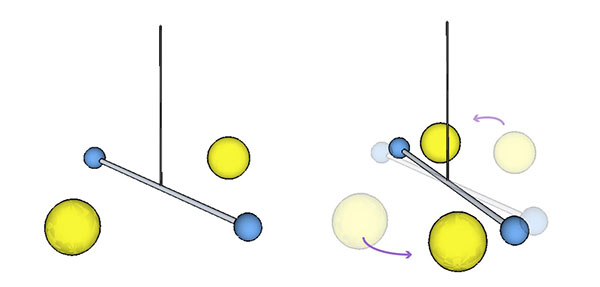
現代版ピサの斜塔の実験に成功!
私たちはこの研究をNewtonプロジェクトと名づけ余剰次元の探索を行っています。プロジェクト最初の装置Newton I号では、センチメートルスケールで重力を測定することに成功し、これをきっかけに、ミリメートルスケールからミクロンスケールでの実験に向けた開発・実験が行われています。
この開発の中で、2号機であるNewton II号では自由落下の一様性から等価原理の検証に成功する成果が得られました。自由落下の一様性は「すべての物質はその種類や組成によらず重力場中で同じ加速度で落下する」という、ガリレオのピサの斜塔の実験で有名なものです。Newton II号の結果は、これまで検証されていなかったセンチメートルスケールにおいて自由落下の一様性を5%の精度で検証することに成功しました。このとき検出した重力の大きさは、地球による重力のわずか1億分の1という微弱な重力であり、ねじれ角度は0.06度以下という非常に小さな変化でした。
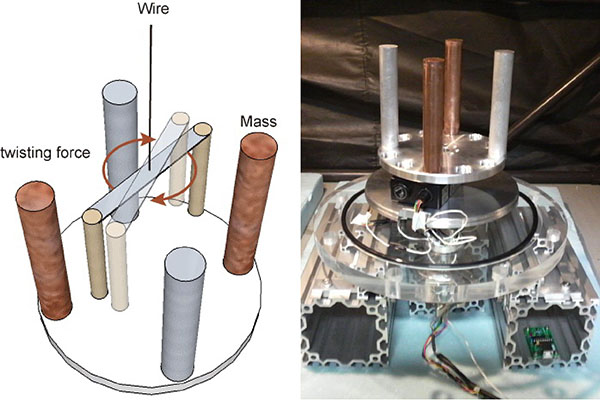
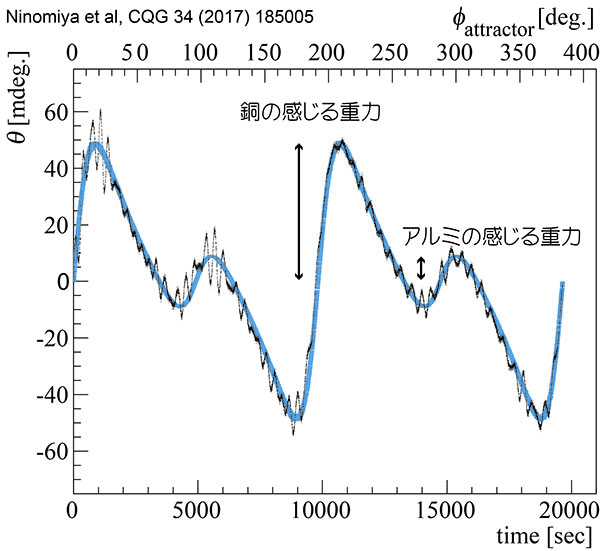
これからが本番
Newton I号から始まったこのプロジェクトは、高感度化、高精度化、そして小型化が進められ現在はNewton V号まで開発が進んでいます。これまでにセンチメートルからミリメートルスケールでの重力測定に成功し、ミクロンスケールでの実験も今まさに進行しています。そのなかで等価原理と万有引力の法則がさらに厳しくテストされつつあります。
今後、近距離で等価原理を破る新たな重力理論の兆候や、余剰次元の存在を示す万有引力の法則の破れなどが発見される可能性もあります。また本研究は大型の研究所での巨大科学ではなく、大学の実験室で学生が主体となって工夫を重ねながら進めているアイディア勝負の小さな実験であり、学生から学生へと代々引き継がれ今回の成果をあげました。
自由落下の一様性の確認は、私たちの実験が正しく重力を捉えている証拠となるテストでもあります。私たちは今回の結果を得て初めて、ミリメートルからミクロンスケールへと重力実験を進める基礎を固めることができたと考えています。今後もこれを足掛かりに本丸の逆二乗則の検証、余剰次元の探索へと、大規模実験に匹敵する大きな成果をあげていきたいと思います。
参考文献
K. Ninomiya et al., “Short-range test of the universality of gravitational constant G at the millimeter scale using a digital image sensor”, Classical and Quantum Gravity 34 (2017) 185005 https://doi.org/10.1088/1361-6382/aa837f
村田次郎 「『余剰次元』と逆二乗則の破れ」 講談社ブルーバックス (2011)
この記事を書いた人

-
二宮一史(写真左)
立教大学先端科学計測研究センター研究員 兼 実践学園中学校・高等学校専任講師
2013年立教大学大学院理学研究科博士課程後期課程単位取得退学。同年立教大学先端科学計測研究センター研究員。聖学院中学・高等学校等にて教員として理科教育に携わり、2016年より実践学園中学・高等学校専任講師。専門は近距離重力の精密検証による余剰次元の探索・等価原理の検証。研究の最前線に立つ者として、物理学を学問として楽しんでもらえるよう、教育活動を行っています。
村田次郎(写真右)
立教大学理学部教授
1999年京都大学大学院理学研究科単位取得退学。博士(理学)。米国ブルックヘブン国立研究所、理化学研究所研究員、立教大学准教授等を経て2012年より現職。カナダ・TRIUMF研究所での原子核を用いた時間反転対称性の研究の他、余剰次元探索のための近距離重力実験など、巨大科学に対抗したアイディア勝負の小規模実験を学生とワイワイ楽しく進めています。
この投稿者の最近の記事
 研究成果2017年10月11日小さな物体にはたらく重力の実験で、4次元以上の異次元空間を探す
研究成果2017年10月11日小さな物体にはたらく重力の実験で、4次元以上の異次元空間を探す



