ゴム風船が割れるとき、大きな音とともに一気に破裂してびっくりした経験は誰しもあると思います。一方で、あまり膨らんでいないゴム風船に針などで穴をあけても、穴はそれほど広がらずゆっくりと空気が抜けていきます。このように、ゴムには高速破壊と低速破壊の2つの破壊形態があります。

低速破壊から高速破壊への変化は「速度ジャンプ」と呼ばれています。速度ジャンプは科学的に面白い現象であるだけでなく、高い耐久性や耐摩耗性を持ったゴム製品の開発にも密接に関係しており、工学的、産業的にも重要な現象です。ところが、速度ジャンプは60年前から知られている現象でありながら、なぜ起きるのかがわかっていませんでした。最近、我々の研究グループでは、ゴムの破壊現象の本質を抽出した「単純な数理モデル」を構築し、その数学的な解をもとにして、速度ジャンプの発生するメカニズムを理論的に解明しました。

ゴムの速度ジャンプとは？

上で述べたようにゴム風船を使って実験すると、風船内部の圧力や風船の形状などさまざまな要素がゴムの破壊に関係します。ここでは問題の焦点を絞るために、下図のようなシンプルな設定の実験を考えます。下図の設定で、最初に与えたひずみ（上下にいくら引っ張ったか）と亀裂（破れ）の進展する速度を測定します。一度の実験でゴムシートは完全に破れるので、破れていない同じゴムシートを用意してひずみを変えながら何度も測定を行い、ひずみと速度の関係を調べます。

速度ジャンプの実験方法。横長のゴムシートを縦方向（短い方向）に引っ張って固定することにより「ひずみ」を与えてから、端に初期亀裂を与えると横方向に亀裂が進展する。しばらくたって亀裂の進展する速度が一定となったときにその速度を測定する

さて、どのような実験結果が得られるでしょうか？　典型的には下図のようになります。

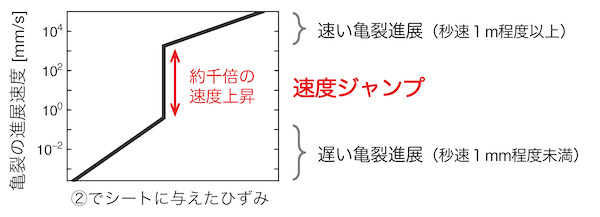
ひずみと速度の関係の両対数グラフ。両対数グラフでは、1目盛りが10倍、2目盛りが100倍、3目盛りが1000倍に対応する。ひずみがある臨界値を超えるときに急激な速度の上昇「速度ジャンプ」が観測される

ひずみを大きくすると速度が大きくなることが予想できると思いますが、実はそれだけではありません。ひずみがある臨界値を超えるときに、数千倍もの急激な速度上昇が起きるのです。これが「速度ジャンプ」です。速度ジャンプを境に、秒速1mm未満の遅い亀裂進展が、秒速1ｍ以上の速い亀裂進展に急激に転移します。このような速度ジャンプは、天然ゴムや合成ゴムで実験条件を変えても観測される普遍的な現象です。しかしながら、1956年に報告されて以来、60年間その発生メカニズムは未解明でした。

亀裂進展を模倣した数理モデルを構築

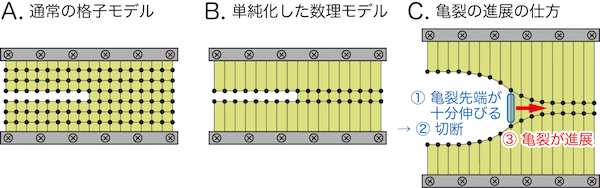
我々は、速度ジャンプが起こるメカニズムを明らかにするために、なるべく単純な数理モデルを構築し、数学的に解析することにしました。もし、単純な数理モデルが速度ジャンプを示せば、そのモデルが速度ジャンプの本質を捕らえていると考えられるからです。我々は、下図Aのような通常よく使われる格子モデルを、下図Bのように亀裂進展問題に特化させて単純化しました。このように単純化しても、下図Cのように亀裂進展を扱えるからです。この単純化により、そのままでは数学的に解けない亀裂進展の問題が解けるようになります。

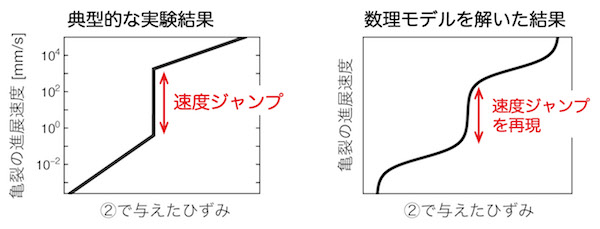
(A) ゴムシートを格子状に並んだ質点（図の黒丸）で代表した標準的なモデル。(B) 本研究で考案した数理モデル。亀裂が進展していく先の質点だけを考えることで、問題が大幅に簡単化される。(C) 亀裂は1〜3の手順を繰り返して右に進む

さらに我々は、上図Bの数理モデルに、ゴムの持つ重要な性質である「ガラス化」の効果を取り入れました。（ガラス化とは、ゴムを速くひっぱると約1000倍硬くなる現象です。次節で詳しく説明します。）すると、この数理モデルの数学的な解から、下図のように速度ジャンプが再現されました。逆に、このガラス化の効果を取り入れない数理モデルを数学的に解くと、速度ジャンプは起こりませんでした。つまり、速度ジャンプの出現にはゴムのガラス化が本質的だとわかりました。

本研究で構築した数理モデルを数学的に解いた結果の両対数グラフ。実験で観測されている速度ジャンプを再現する

ゴムは速くひっぱると1000倍硬く振る舞う

ここで少し脱線して、ゴムを速くひっぱると硬くなる現象「ガラス化」について説明します。ゴムは、とても長いひも状の高分子の集まり（生ゴム）を、加硫と呼ばれる化学反応によって結びつけた物質です。たとえるなら、茹でたてのざるそばの一本一本が、ところどころ結びついていてひとつの塊になっているような物質です。ただし、ゴムのひも状高分子は、ざるそばと違ってミクロな分子であるため、激しい熱運動をしています。つまり、「激しく熱運動するざるそば」というのが、分子レベルでのゴムの正しいイメージです。このために、ゴムはひっぱる速さによって異なる3つの性質を示します。

まず、ゴムをゆっくりひっぱると、しなやかに熱運動するひも状高分子を引き延ばすことになり、我々が日常的に目にする柔らかいバネのように振る舞います。次に、ゴムを少し早くひっぱると発熱します。（たとえば、輪ゴムを早くひっぱると発熱が確かめられます。）最後に、熱運動よりも速くひっぱると、ゴムを構成するひも状高分子は熱運動できずに硬い棒のように振る舞い、ゴムはガラスのように硬くてもろい状態になります。この状態になることを「ガラス化」と言います。これは、茹でる前の乾燥したざるそばが硬くて脆いことに対応します。

速度ジャンプの起源は「亀裂先端のガラス化」

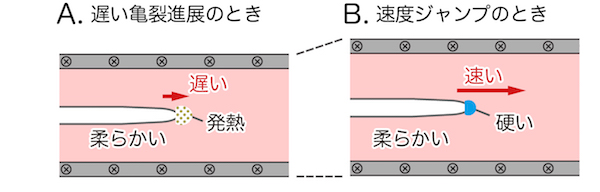
我々は、今回構築した数理モデルを数学的に詳細に分析することで、60年前からの謎であった速度ジャンプが起こるメカニズムを明らかにしました。遅い亀裂進展のときには、下図Aのようにゴムシート全体が柔らかいままで、亀裂先端だけは少し早くひっぱられるので、発熱しながらゆっくりと亀裂が進展していきます。ところが、亀裂の進展速度がある限界値に達すると、下図Bのように亀裂の先端でゴムの「ガラス化」が起こり、それにより速度ジャンプが起こって一気に裂けるのです。たとえば、柔らかいプラスチックはゆっくりとしか引き裂けませんが、硬いガラスは一瞬で粉々になるのと同じです。

速度ジャンプの発生メカニズム。(A)低速破壊では、亀裂先端が発熱しながら亀裂が進展していく。(B)速度ジャンプは、亀裂先端が非常に速く引っ張られることにより、ガラスのように硬くなることによって引き起こされる

なぜ速度ジャンプのメカニズムがこれまで未解明だったのか不思議に思うかも知れません。実は、ゴムの亀裂進展の問題は数学的な取り扱いが非常に難しいため、上記のようなメカニズムの説明を与える理論は存在しませんでした。今回は、大幅に単純化した数理モデルを新しく構築することで、数学的な困難を避けてメカニズムを説明することに成功したのです。

今回の理論は速度ジャンプの起源を明らかにしただけではなく、速度ジャンプの起こりづらい丈夫なゴムを開発するための指針も示しました。速度ジャンプを抑制するには、ゴムを構成するひも状高分子の網目を粗くすること、および、ガラス化したときの硬さを強化すれば良いことが数式で示されました。特に、網目を粗くすることが速度ジャンプの抑制につながることは、過去の実験結果によっても裏付けられています。これらの指針に基づけば、材料開発のトライアルアンドエラーが抑えられ、耐久性や耐摩耗性の向上したタフな新規ゴム材料の開発を効率的に行うことができると期待されます。

参考文献：N. Sakumichi and K. Okumura, “Exactly solvable model for a velocity jump observed in crack propagation in viscoelastic solids”, Scientific Reports 7, 8065 (2017). doi:10.1038/s41598-017-07214-8

この記事を書いた人

作道直幸
作道直幸
お茶の水女子大学・特任助教。2012年京都大学大学院理学研究科修了。博士(理学)。東京大学、理化学研究所を経て、2015年より現職。理論物理学の万能選手を目指している。これまでに、素粒子物理、量子統計力学、化学物理、ゴムの物理など、対象を限定せずに幅広く物理学全般の研究に従事してきた。研究手法は、紙とペンだけを用いた解析計算から、スーパーコンピューターを用いた大規模数値シミュレーション（量子モンテカルロ計算、格子ゲージ理論）まで使える物は何でも使う。最近は、これまで理論物理学者があまり目を向けてこなかった工学系、材料系などの問題について、物理の視点から分野横断的に解決することに興味を持っている。http://researchmap.jp/sakumichi/