地球はやっぱり丸かった?!- 物質を最適な方法で運ぶ理論を用いて物の形を理解する
こんにちは、首都大学東京の高津飛鳥です。首都大学東京は京王相模原線の南大沢駅が最寄り駅です。京王線は主に東京(たまに神奈川)を東西に走る電車で、東端は新宿駅です。そして大体真ん中の調布駅で相模原線と分岐し、そして南大沢を通過するとすぐに西端の橋本駅です。
突然ですが問題です!
橋本と調布にパン工場があり、これらを我らが南大沢と新宿の喫茶店に運びます。橋本と調布からはともに200個のパンを出荷し、そして南大沢には150個、新宿には250個のパンを入荷します。パンひとつあたりの輸送費用が 橋本から南大沢は1円、橋本から新宿は4円、調布から南大沢は2円、調布から新宿は1円 であるとき、一番安く運ぶ方法(最適解)は何でしょうか?
問題を図で書くと以下のようになります。
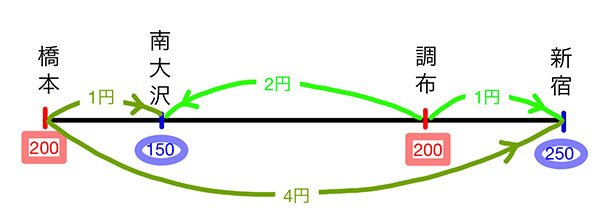
感覚として近くに運ぶと安いと知っているので
橋本→南大沢:150個、調布→南大沢:0個、橋本→新宿:50個、調布→新宿:200個
という運び方が最適で、輸送費用は550円だとわかります。しかしこれが最適だという根拠が直感だけでは心許ないので、連立方程式による厳密な証明を考えてみましょう。
橋本から南大沢に?個、調布から南大沢に?個運ぶとすると、橋本から新宿に(200 − ?)個、調布から新宿に(200 − ?)個運ぶことになります。このとき? + ? = 150に注意すると、輸送費用は
1 × ? + 2 × ? + 4 × (200 − ?) + 1 × (200 − ?) = 1000 − 3? + ? = 550 + 4?
となります。そして0 ≤ ?, ? ≤ 150なので、輸送費用は? = 0のとき最も安い550円となります。
このように出荷地と入荷地の数が少ないときは直感が働き、連立不等式を解くこともそんなに難しくありません。しかし出荷地も入荷地もたくさんありその配置が複雑な場合は、直感は働きづらく、そして未知数が増えるため連立不等式を解くことも大変になります。
たとえば秋の味覚、梨を運んでみましょう。相模原線沿線では京王稲田堤の付近で梨狩りができ、稲田堤では相模原線と立川と川崎を繋ぐ南武線が十字に交差しています。そこで梨を立川・稲田堤・川崎の3か所から橋本・南大沢・調布の3か所に以下の量と費用で運ぶとき、最適解は何でしょうか?
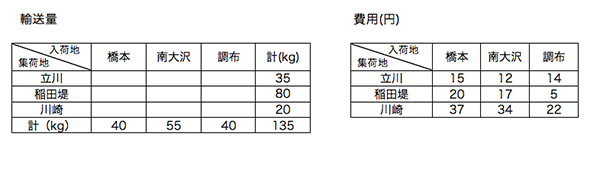
これを漠然とした直感(や連立方程式で)解くのは大変なので、「近くに運べば安い」と直感を数学の言葉で表し確固たる理論にし、そしてその理論に基づき最適解を探してみましょう。
北西隅法とモンジュ性
出入荷地が沢山あっても、それらが横に一直線上に並んでいれば近くへ運ぶ方法は簡単に決められます:左端の出荷地から左端の入荷地へ運び、出荷地が空になったら右隣の出荷地に、入荷地が一杯になったら右隣の入荷地に移りどんどん運べば良いのです。この近場へ順々に運ぶ方法は、表の左上のマスから目一杯どんどん埋めていく方法として一般化され、「北西隅法」と呼ばれます。
ここで、表の左端には出荷地が縦に、上端には入荷地が横に書かれているとします。そして北西隅法が最適解であるためには表の並びが近い順である必要があり、それは「費用がモンジュ性を満たす」ことで定義されます。出荷地が?個、入荷地が?個あり、表の上から?番目の出荷地から、表の左からj番目の入荷地への輸送費用が???円であるとき、この費用がモンジュ性を満たすとは任意の1 ≤ ? < ? ≤ ?, 1 ≤ ? < ? ≤ ?に対し
??? + ??? ≤ ??? +???
が成り立つことです。たとえば、? = ? = 2ならば ? = 1, ? = 2, ? = 1, ? = 2の場合のみを考えれば良いので
?11 + ?22 ≤ ?12 + ?21
が成り立つとき、費用はモンジュ性を満たします。そして実際に、費用がモンジュ性を満たすならば北西隅法が最適解になります。たとえば、最初のパンを運ぶ問題の最適解を、北西隅法を用いて考えてみましょう。
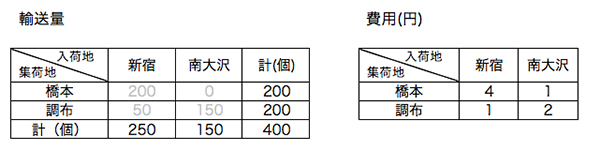
これは最適解でありませんが、それは費用がモンジュ性を満たさないからです。そこで表の新宿と南大沢の位置を変えれば費用はモンジュ性を満たし、このときの北西隅法は最適解になります。 ちなみに梨の輸送費用もモンジュ性を満たしているので、北西隅法が最適解となります。しかし費用によってはどのように並び替えてもモンジュ性を満たさないものがあります。そのような場合は北西隅法を飛び石法により改善することで、最適解が得られることが知られています(たとえば梨を運ぶ問題で、川崎から橋本への輸送費用を37円から36円にすると、どのように並び替えても費用はモンジュ性を満たしません)。
物を運ぶと形がわかる
では パンのような固体ではなく、水のような物質を輸送する場合はどのような輸送が最適解となるでしょうか? たとえば、円盤状の水たまりを他の場所に移すとします(ただし最初と最後の円盤の形は同じとします)。このとき平行移動が最適な輸送に思えます。実際、輸送費用が距離の二乗に比例するときは、最短線に沿った輸送が最適となります。そこで平面上では平行移動による輸送が最適となり、そして水の形は元の円盤の形を保ったまま運ばれます。
しかし地球は平面ではなく曲がっています。たとえば水を北極から南極へ運ぶとすれば、北極と南極を通る最短線は経線なので、経線に沿った輸送が最適となります。そして北極(点)と南極(点)の中点がなす集合が赤道全体(曲線)になるように、輸送途中の水の形は元の円盤の形と異なり、特に途中経過のどこの水の形を見ても元の円盤よりも広がっています。これは地球が正に曲がっていることにより起きる現象です(ちなみに途中経過のどこの水の形を見ても元の円盤よりも縮まる空間は負に曲がっていると考えられ、その代表例は双曲平面と呼ばれる曲面です)。
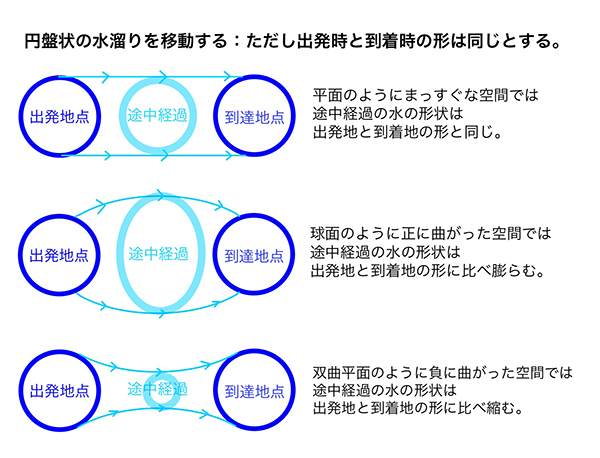
このように物質を最適な方法で運ぶことで、私たちは宇宙に出ることなく地球上にいるまま、地球が正に曲がっていることを知ることができます(しかし丸いかどうかはこれだけではわかりません)。
私の研究は、このような理論(最適輸送理論)を用いて物の形や形ごとに定まる性質を調べること(幾何解析)です。
参考文献
1. R.E.Burkard, B.Klinz, R.Rudolf,“Perspectives of Monge properties in optimization”,Discrete Appl. Math.(1996),95—161.
2. 刀根 薫, “オペレーションズ・リサーチ読本(増補版)”, 日本評論社(1991).
3.桑江一洋,塩谷隆,太田慎一,高津飛鳥,桒田和正,“最適輸送理論とリッチ曲率”, 日本数学会 (2017).
この記事を書いた人

- 学部入学から学位を取るまでずっと杜の都・仙台にいたので、仙台人とよく間違えられるが「いづい/いずい」が使いこなせない関東人。しかし仙台生活後にフランスで1年過した際に、東北人が得意と言われる鼻母音が割と得意だと気付く。その後、ドイツで1年過したが全くアルコールに強くならないまま帰国。そして名古屋で自転車をケッタと呼ぶことに驚く生活を経て現職(首都大学東京 理工学研究科 数理科学情報専攻 准教授)に就く。来年から改組により研究科名と専攻名が変わる予定。