準結晶と幾何学モデル

古代ギリシアのミロのヴィーナスや、レオナルド・ダ・ヴィンチのモナ・リザといった芸術作品に対し、我々が美しさを感じるのはなぜでしょうか？ これらの作品のなかには、「黄金比」と呼ばれる、ある数学モデルから導き出される、特徴的な数が潜んでいるからとされています。黄金比τ（タウ）は、フィボナッチ数列（1, 1, 2, 3, 5, 8,…）の隣り合う2つの数の比の極限値であり、1.618…という無理数です。この比率1：1.618…は、最もバランスのとれた長方形の縦横比とされており、数々の建造物やロゴなどに用いられています。こうした一見人工的な数である黄金比τが、自然界にも潜んでいるとしたら驚くべきことではないでしょうか？ その一例が「準結晶」と呼ばれる物質です。

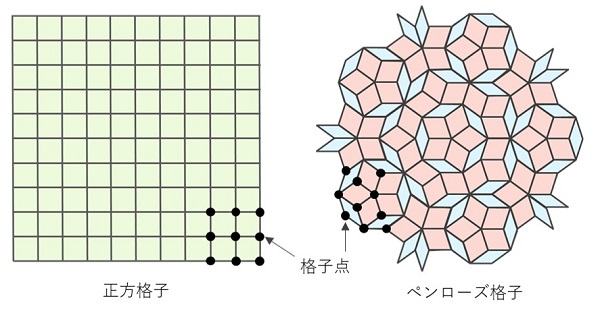
準結晶は固体の一種ですが、いわゆる通常の「結晶」とは、その構造の持つ性質が異なります。通常の結晶（周期結晶）は、「並進対称性」という性質を持ちます。たとえば、「正方格子」と呼ばれる「格子点」は、下図のように面全体を埋め尽くしています。これら格子点の全体は、ひとつの正方形を縦横にずらすことによって作り出せます。このように、単位となる多角形を縦横に並べて作り出される格子点の集合（今の例では正方格子）は、（数学の言葉を使うと）「並進対称性を持っている」と表現されます。

一方、準結晶の構造モデルのひとつである「ペンローズ格子」は（τ倍の面積比を持つ）2種類の菱形で構成されますが、これらを縦横にずらして並べても、それを作り出すことはできません。この理由により、「ペンローズ格子は並進対称性を持たない」といわれます。なお、ペンローズ格子を発見したR・ペンローズは、ブラックホールの研究でノーベル物理学賞（2020年）を受賞されました。

また、結晶は「回転対称性」という性質も持っています。たとえば先ほどの「正方格子」の場合には、ある格子点を中心に90°回転させると、元の状態と完全に一致させることができます。幾何学を使って調べると、結晶に許される回転角は、90°のほかに60°、120°およびそれらの整数倍（たとえば180°など）であることがわかっています。一方、ペンローズ格子には、周期結晶では許されない、72°といった特別な回転操作が許されます。また、ペンローズ格子には、フラクタル性と呼ばれる、スケールをτ倍拡大しても似た構造が現れる性質を持ちます。このように準結晶の構造には、通常の結晶には見られない幾何学的な特徴がいくつも含まれているのです。

（左）正方形を並べて作られる正方格子。格子点（黒丸）は縦横に等間隔に並んでいる。（右）黄金比τを面積比に持つ、2種類のひし形を並べて作られる2次元ペンローズ格子。ペンローズ格子は、並進対称性を持たず、5回回転対称性、黄金比τ倍でのスケール変換といった、通常の周期格子とは異なる性質を持つ。

多面体がつくり出す原子集団

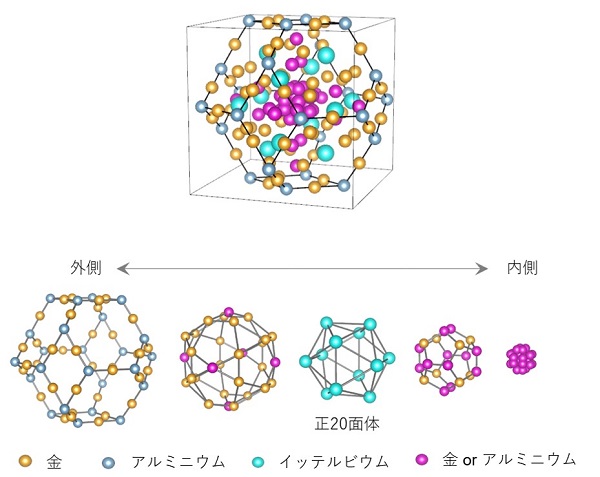
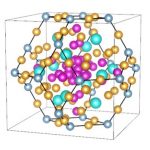
通常の結晶（周期結晶）は、正方格子のように周期的に並んでいる格子点上に、（ひとつもしくは複数個の）原子が配置されます。準結晶の場合も同様で、2次元準結晶の場合には、ペンローズ格子に代表される、「準周期的」に並んでいる格子点（準格子点）上に、原子が配置されます。各準格子点に並ぶ原子についても、準結晶は変わった特徴を持ちます。準結晶中の原子は、「多面体クラスター」と呼ばれる100個程度の集団を形成します。このクラスターは、正4面体や正12面体、正20面体といったさまざまな多面体が、ロシアのマトリョーシカ人形の様に、入れ子状に重なり合っています。これらの多面体クラスターが、準格子点上に並んでいるものが準結晶です。

一方、正方格子のような周期格子上に、準結晶と同じ多面体クラスターが並ぶ物質が存在し、これを「近似結晶」と呼びます。近似結晶は、準結晶と同じ局所構造（多面体クラスター）を持つとともに、並進対称性（周期性）をも持っています。なお、近似結晶にも種類があり、1/1近似結晶、 2/1結晶などと呼ばれます。ここで、1/1や 2/1などの分数は、無理数である黄金比を近似する数列（フィボナッチ数列と関係）、1/1, 2/1, 3/2, 5/3, ……に由来しています（これらの有理分数が黄金比を近似するものであることから、それに対応する物質は近似結晶と呼ばれています）。ここにも、数学と物質との不思議な関係を見て取ることができます。

一口に準結晶といっても、準格子の種類や、そこに配置される原子クラスターの種類はさまざまです。たとえば、現在我々が研究している、金・アルミニウム・イッテルビウムの3種類の元素で構成される準結晶においては、イッテルビウム原子（希土類元素のひとつ）が、正20面体を形成します。以下に紹介するように、我々が最近発見した準結晶・近似結晶の不思議な性質に対して、正20面体中のイッテルビウム原子が重要な役割をしていることがわかってきました。

準結晶や近似結晶を構成する原子クラスターとその内部構造。さまざまな多面体が、入れ子状に重なり合っている。物質の性質（磁性など）の主役を担うイッテルビウム原子は、外側から3つめのシェル（正20面体）を形成する。

ミクロな構造とマクロな性質の関係

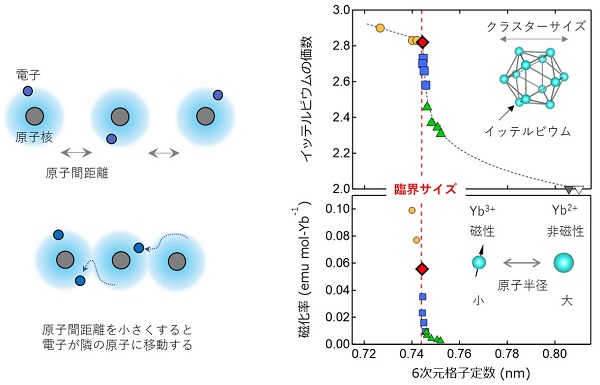
イッテルビウムに代表される希土類元素は、他の元素に比べて変わった価数状態をとることが知られています。たとえば、食塩に含まれる塩化ナトリウム（NaCl）中のナトリウムイオンは+1価、塩化物イオンは-1価というように、通常は整数の価数をとることが多いですが、イッテルビウムイオンは、+2.7のような非整数の価数をとることがあります。これは、希土類元素中の電子が、他の元素の電子と部分的に混ざり合う（混成する）ことによって起こります。そして、このような混成の程度は、試料に対して外部から強い圧力を加えたり、構成元素の比率を調整したりすることで、連続的に変えることができます。

我々は、準結晶や近似結晶を構成する金とアルミニウムを、原子半径の異なる他の元素で置き換えることで、試料に対して実効的な圧力を加えることを試みました。その結果、さまざまな格子定数（長さの単位を持ち、クラスターの大きさに対応する）を持つ準結晶・近似結晶を得ることができました。これらの準結晶・近似結晶に対し、イッテルビウム原子の価数と磁気的性質を精密に調べた結果、格子定数を連続的に変えているにもかかわらず、価数が急激に変わる特徴的な値（臨界サイズ）が存在することがわかりました。そしてその臨界サイズにおいては、磁気的性質も同様に特異的に変わることが明らかになりました。特に磁化率の変化量は非常に激しく、格子定数をわずか1000億分の1メートル（10ピコメートル）変えただけで、30倍程度もの変化をすることがわかりました。

（左上）孤立した原子における電子雲の広がり。（左下）原子間距離を小さくすることにより、電子が隣の原子に移動する。（右上）準結晶中のイッテルビウム原子の価数と6次元格子定数（クラスターサイズに対応）の関係。臨界サイズを境に、価数が急激に変化する。（右下）磁化率と6次元格子定数の関係。同じ臨界サイズにおいて、磁化率は1桁以上もの大きな変化を見せる。

こうした特徴的な変化は、準結晶だけではなく同じ多面体クラスターを持つ近似結晶でも同様に観測されました。つまりこの性質は、クラスターの配列の仕方（周期性か準周期性か）には依存しない、クラスター固有のものであることを意味しています。我々は、準結晶と近似結晶の比較研究をとおして、原子クラスターのミクロな性質（サイズ）とマクロな磁気的性質を繋ぐ新しい関係を発見しました。

固体中の量子相転移

氷が溶けて水になる様子は、我々が日常よく目にする相転移のひとつです。また、フェライト磁石に代表される永久磁石は、加熱をすることで磁石としての性能を失います。これも相転移のひとつです。これらはいずれも有限温度で見られる現象ですが、絶対零度（-273.15℃）で起こる相転移も存在します。これを「量子相転移」と呼びます。

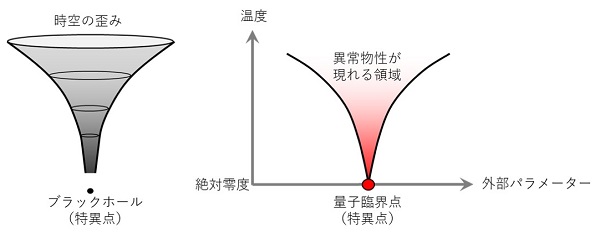
固体中の量子相転移は、ブラックホールとのアナロジーとして捉えることができます。ブラックホールは数学的な特異点ですが、その影響は広範囲におよび、周囲の時空を歪ませます。こうした現象は重力レンズ効果をとおして観測することができます。同様に、固体中に存在する量子相転移も、（実験的に到達不可能な）絶対零度における特異点ですが、その影響は有限温度にまで広がり、電気伝導や磁性といった性質にさまざまな異常を生じさせます。これらの観測可能な物理量をとおして、我々は量子相転移の研究を行うことができるのです。

本稿で紹介した、金・アルミニウム・イッテルビウム準結晶は、こうした量子相転移を起こす特異点（量子臨界点）を持つことが指摘されていました。今回我々が発見した、価数や磁性の特徴的な変化は「価数ゆらぎ」という量子力学的な性質を起源に持つ、量子臨界点が存在することを強く証拠付けるものです。

宇宙のブラックホールと固体の量子臨界点のアナロジー。数学的な特異点であるブラックホールの周囲の時空が歪むのと同様に、絶対零度における特異点である固体中の量子臨界点も、有限温度の物性に対してさまざまな影響を与える。

このように準結晶は、美しい幾何学構造を持つと同時に、基礎物理学的にも興味深い性質を多く含んだ大変魅力的な物質です。準結晶の研究分野は、他のさまざまな分野とも深い関わりを持っており、今後は新しい融合研究が生まれることでしょう。これらの未踏の領域を共に切り拓いてみませんか？

参考文献
Concomitant singularities of Yb-valence and magnetism at a critical lattice parameter of icosahedral quasicrystals and approximants.
Scientific Reports 10, 17116 (2020), DOI：https://doi.org/10.1038/s41598-020-74124-7
Keiichiro Imura, Hitoshi Yamaoka, Shinjirou Yokota, Kazushi Sakamoto, Yoshiya Yamamoto, Takuma Kawai, Keisuke Namba, Shinnosuke Hirokawa, Kazuhiko Deguchi, Nozomu Hiraoka, Hirofumi Ishii, Jun’ichiro Mizuki, Tsutomu Ishimasa, and Noriaki K. Sato

この記事を書いた人

井村 敬一郎
井村 敬一郎
名古屋大学　大学院理学研究科　助教
名古屋大学大学院理学研究科博士課程修了後、日本学術振興会特別研究員、分子科学研究所博士研究員を経て2012年より現職。結晶育成、高圧・低温物性、分光などの実験手法を用い、物質を構成する原子の電荷（価数）揺らぎが引き起こす、新しい物理現象の解明を目指して研究を進めています。