「超伝導」と「トポロジカル超伝導体」

超伝導とは、金属や化合物の電気抵抗がある温度以下で急激にゼロになる現象のことです。抵抗がない超伝導体は、大きな電流を流して強い磁場を発生させることができるため、すでに医療機器のMRIやリニア新幹線といったさまざまな用途に使われています。近年では量子コンピュータの基本素子にも超伝導を使ったものが考案されています。

これまでに発見されている超伝導を示す物質は、常圧（つまり、我々が生活している大気圧）では非常に低い温度でしか超伝導にならず、その温度は最も高いものでもなんと約-140℃です。これでは使い勝手が悪いため、より高い温度で、できれば室温でも超伝導となる物質を探す研究が世界中で行われています。

このような超伝導となる温度を高める研究とは別に、超伝導に関していま世界中で熱い競争が繰り広げられている研究テーマとして「トポロジカル超伝導体」が挙げられます。トポロジカル超伝導体という聞き慣れないキーワードが登場しましたが、超伝導体がトポロジカルであるとは一体どういうことなのでしょうか？

「トポロジー」とは何か

身の回りの物質の性質を調べる「物性物理学」において、「トポロジー」の重要性はこの四半世紀で急速に認識されるようになりました。2016年には「物質のトポロジカル相転移とトポロジカル相の理論的発見」という功績に対して米国の物理学者3名にノーベル物理学賞が授与され、脚光を浴びました。

ここではこのトポロジーについて、コーヒーカップ、ドーナッツ、ボールの例をとおして説明したいと思います。イメージをしやすくするために、粘土でできたコーヒーカップを想像してみましょう。粘土をちぎったり穴を開けたりしなくても、グニャグニャと変形していくだけでコーヒーカップをドーナッツの形に変形できることが想像できるでしょうか？ コーヒーカップの取手の輪っかがドーナツの輪に対応します。このような滑らかな変形を「断熱変形」といい、断熱変形できるもの同士はトポロジーの考え方では「同じ」だとみなして分類します。

一方、粘土のドーナッツをボールへと変形するには、途中で穴をつぶすという大胆な操作が必要になります。つまりドーナッツはボールへと断熱変形することはできないので、ボールとは「違う」ということになります。この例で「穴の数」は滑らかな変形の過程で変わらないので「トポロジカル数」と呼ばれます。

トポロジカル超伝導体を見つけるには？

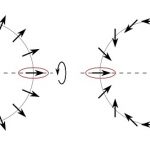
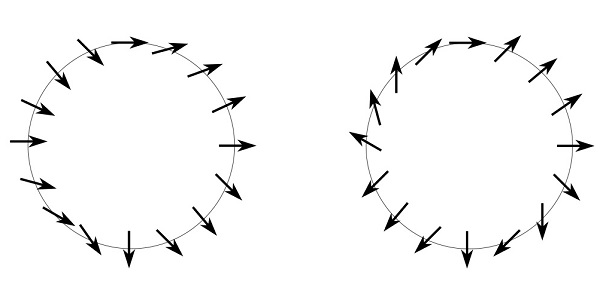
物性物理学においてもトポロジーはさまざまな場面に登場します。最も簡単な例として、下図のように円周上に等間隔に並んだ電子のスピン（ここでは矢印で表現します）の向きに着目してみましょう。隣り合うスピン同士はほぼ同じ向きを向いているとします。このような場合、円周を1周したときにスピンが何回転するかという「巻きつき数」を考えることができます。

下図の右の例では、スピンは円周1周のあいだに1回転するため巻きつき数は1です。一方、左の例では基本的に右を向いており一度も回っていません。巻きつき数はスピンの向きを滑らかに変えても変わらないのでトポロジカル数です。

超伝導体に対しても穴の数や巻きつき数のようなトポロジカル数を考えることができ、0でないトポロジカル数を持つものは「トポロジカル超伝導体」と呼ばれています。

近年の研究によって、トポロジカル超伝導体の表面には次世代の量子コンピューターの素子への応用が期待される「マヨラナ粒子」が現れることがわかっており、注目を集めています。しかし世界中の研究者による精力的な研究にも関わらず、現在までにトポロジカル超伝導となることが確認されている物質はほとんどないのが現状です。

数え切れないほど多様な物質が存在するなか、トポロジカル超伝導体の候補となる物質は闇雲に探しても見つかるようなものではないため、探索を進めるうえでの指針を確立することが急務となっています。さらに、具体的な候補物質に対して「穴の数」や「巻きつき数」といったトポロジカル数を実際に計算することは困難で、これが物質の探索を困難にしていました。

結晶の対称性からトポロジカル数を判定する

そこで私たちは、超伝導体の持つ結晶の対称性に着目することで、その超伝導体が持つトポロジカル数を簡単に判定する手法を開発しました。

結晶にはさまざまな対称性が存在します。たとえば高校化学で習う塩の結晶は軸周りに90度回転させたり、ある面に対して反転させるなどの操作に対して不変です。3次元結晶の対称性の組み合わせは230種類に分類されており、これらの対称性は物質中の電子状態を理解するのに古くから利用されていました。

最近の研究によって、結晶対称性はトポロジーを理解するうえでも有用であることが明らかになってきました。結晶の対称性がある場合には、物質の全体をみなくともごく少数の自由度に着目するだけでトポロジーを大雑把に判定することができるのです。

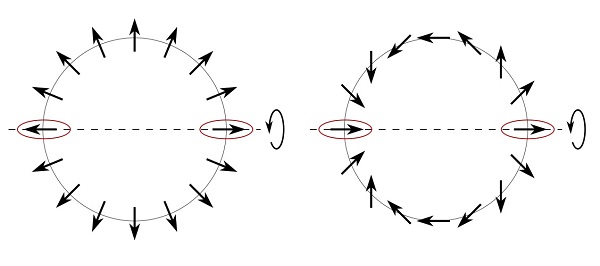
例として再び円周上のスピンの巻きつき数を考えます。ここではさらに図の点線で示した軸のまわりに180°回転しても変わらないという対称性を課してみましょう。すると回転軸上の2点のスピン（下図の赤丸で囲んだもの）は、回転軸に沿って同じ向きか反対向きかの2通りの場合しか存在しません。実はこの2点のスピンの向きを見るだけで、巻きつき数が偶数か奇数かを判定することができます。

同じ向き（下図の右）の場合には、スピンは必ず偶数回回転します。一方で反対向きの場合（下図の左）、矢印の回転数は奇数でなければなりません。この場合は、特に巻きつき数は0となることができず、必ず非自明なトポロジーを持たねばならないことがわかります。

超伝導体にもさまざまな結晶対称性が存在するため、同様の性質を利用してそのトポロジーを簡便に判定することができるのです。我々はこのアイディアを推し進めて論文に発表しました。近年流行のデータ駆動的な物質探索と組み合わせることで、トポロジカル超伝導体候補物質が発見され、将来的な量子コンピュータの実用化につながることを期待しています。

誌面の都合上、込み入った議論はできませんでしたが、より詳細な内容が気になる方は、下記の参考文献から、原論文もしくは日本語による解説記事を参照していただけますと幸いです。

参考文献

この記事を書いた人

小野 清志郎. 渡邉 悠樹
小野 清志郎（おの せいしろう）
東京大学大学院工学系研究科物理工学専攻 博士課程1年
東京大学理学部物理学科卒業後、同大学大学院理学系研究科物理学専攻にて修士課程を修了し、令和元年度理学系研究科研究奨励賞を受賞。2020年度より工学系研究科物理工学専攻博士課程に在籍中。また、2020年度より学術振興会特別研究員 (DC1)。物性物理を専攻しており、現在の興味はトポロジカル超伝導体の系統的理解。

渡辺 悠樹（わたなべ はるき）
東京大学大学院工学系研究科物理工学専攻 准教授
1986年生まれ。東京大学理学部物理学科卒業後、カリフォルニア大学バークレー校へ留学しPhDを取得。マサチューセッツ工科大学研究員などを経て2019年より現職。南部ゴールドストーン定理を一般化する研究成果で⻄宮湯川記念賞、トポロジカル物性に関する研究で凝縮系科学賞などを受賞。専門は物性理論。物性物理における普遍的物理法則の探究に興味がある。