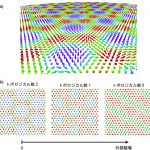
高いトポロジカル数をもつ磁気スキルミオンを発見 – 超小型メモリデバイスの開発に向けて
私たちの研究グループでは、物質中の電子の振る舞いを理論的に調べています。電子は、ミクロな荷電粒子であるとともに磁石としての性質を持ちます。そのため、電子の振る舞いを調べることで、物質が示す電気伝導性や磁性、あるいはその両方が関わる磁気伝導現象などを解明することができます。こうした性質に基づく電子工学(エレクトロニクス)の技術は、コンピューターデバイスに活用されるなどして、現代社会の基盤を支えてきました。機能性がさらに高い物質の開発や未知の性質の開拓は、社会に画期的な変革をもたらす可能性があるため、精力的な研究が続けられています。とりわけ、磁気スキルミオンという数学のトポロジーを用いて特徴づけられる磁気構造は、次世代の情報メモリ素子などとして応用できる可能性があるため、大きな注目を集めています。
今回の研究では、従来調べられてきたトポロジカル数1の磁気スキルミオンとは異なるトポロジカル数2の磁気スキルミオンを見出しました。さらに、外部磁場によってトポロジーの多段スイッチングが可能であることも明らかにしました。
トポロジーとは?
トポロジーは幾何学の一分野です。しかし、トポロジーと高等学校までで習うユークリッド幾何学とは、「2つの図形が同じであるとみなす」基準に関して大きな違いがあります。ユークリッド幾何学では、「合同変換」で移り合う図形同士を同じとみなします。一方、トポロジーでは、その基準は緩く、「連続変形」で移り合える図形同士を同じとみなします。そのため、トポロジーでは、2つの図形が同じか否かをどのように判別するか、というのが基本的な問題です。それに対する有効的なアプローチのひとつに、連続変形では変化しない「トポロジカル数」というものをそれぞれの図形に対して定義するという方法があります。トポロジカル数の代表的な例は、図形の穴の数やひねり数です。
たとえば、アルファベットの形をトポロジーで区別するときには、穴の数が重要な役割を果たします。「C, E, F」などはトポロジカル数(穴の数)が0、「A, D, O」などはトポロジカル数が1、「B」はトポロジカル数が2です。別の例として、普通の帯とメビウスの帯とを区別するときには、帯が何回ひねられているかが良いトポロジカル数になります。普通の帯ではトポロジカル数(ひねり数)が0ですが、メビウスの帯ではトポロジカル数が1です。
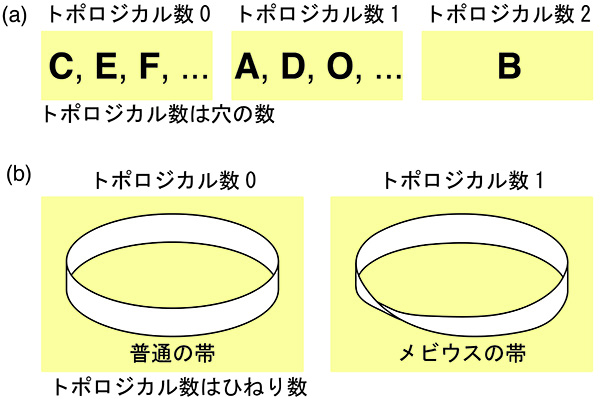
(b)トポロジーによる普通の帯とメビウスの帯の区別
今回の研究テーマである磁気スキルミオンは、上述の例のようにトポロジカル数で特徴づけられる電子の磁石の配列構造です。
磁気スキルミオン
磁気スキルミオンは、電子の磁石の向きが渦状に並んだ構造を持っています。この磁気渦構造に対するトポロジカル数は、すべての矢印の矢尻を束ねたときに矢の先が球面を何回覆うか、という量で定義されます。下図の例では、(b)に示すように球面をちょうど1回覆う形になるので、トポロジカル数は1となります。
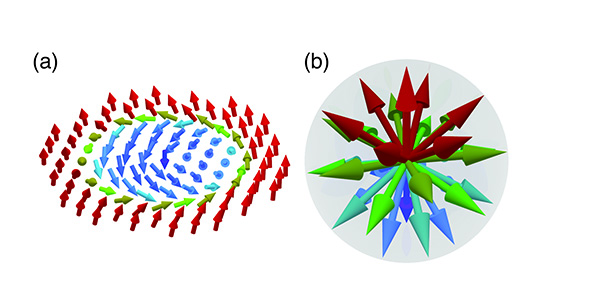
(b)球面をちょうど1回覆う形になるためトポロジカル数は1となる
トポロジカル数は、連続変形に対して不変であるため、磁気スキルミオンは熱ゆらぎや不純物効果に対して堅牢であることが期待されています。そのため、磁気スキルミオンのトポロジカル数をデジタル情報として取り扱うことができれば、磁気スキルミオンを新たな不揮発性メモリ素子として応用できる可能性があります。この技術を応用することができれば、メモリ素子に必要な物理的領域のサイズが大幅に小さくなるため、小型の不揮発性メモリデバイスの開発などが期待できます。
これまでの研究では、主に空間反転対称性が破れた物質を磁場中に置いたときに現れるトポロジカル数1の磁気スキルミオンが調べられてきました。ところがごく最近になって、空間反転対称な物質や理論モデルにおいても磁気スキルミオンが見出され、その安定化機構が議論の的になっています。こうした磁気スキルミオンには従来と異なる性質が期待されることから、応用の幅がさらに広がる可能性があります。そのため、このような新しいタイプの磁気スキルミオンの探索が世界的な研究の潮流となっています。
理論モデルと大規模数値シミュレーション
私たちの研究グループでは、新しいタイプの磁気スキルミオンの発見を目指して、金属磁性体に対する基本的な理論モデルにおいて安定化する電子の磁石の配列パターンを解析しました。そのために、近年開発された効率の良いアルゴリズムを適用し、超並列スーパーコンピューターを用いることで、大規模な数値シミュレーションを行いました。物質中における電子の振る舞いは多数の電子同士の協調現象によって決まるため、このような大規模な数値計算が本質的に重要となります。
トポロジカル数2の新しい磁気スキルミオン
数値シミュレーションの結果、金属磁性体においてトポロジカル数2の磁気スキルミオンが現れることを見出しました。これは、これまでのトポロジカル数1の磁気スキルミオンとは異なるまったく新しいものです。また、従来の磁気スキルミオンを安定化させるのに必要であった物質の空間反転対称性の破れや磁場を必要としないため、磁気スキルミオンを実現させる物質の候補が広がります。さらに、このような新しい磁性が系全体の電子の複雑な協調現象によって起きていることを見出しました。
さらに、磁場中に置くことによって、トポロジカル数2の磁気スキルミオンがトポロジカル数1の磁気スキルミオン、トポロジカル数0の磁気渦状態への多段階の変化が生じることを見出しました。このようにトポロジカル数が2→1→0と多段階に変化する振る舞いは、従来の磁気スキルミオンには見られないまったく新しいものです。
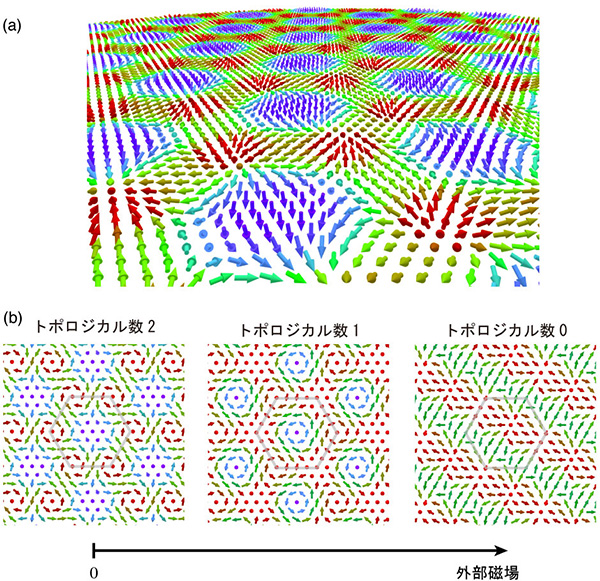
(b)磁場中に置くことでトポロジカル数が2→1→0と多段階に変化する
この現象は、磁気スキルミオンのトポロジカル数をデジタル素子として応用するときに、顕著な利点になる可能性があります。なぜなら、従来の磁気スキルミオンはトポロジカル数が0と1をとることで2値メモリとしての機能が期待できましたが、今回の研究で見出された磁気スキルミオンは多値メモリとしての機能を有することが期待できるからです。これを応用することで、新しいタイプの超小型メモリデバイスの開発などが期待できます。
磁気スキルミオンは次世代技術としての応用が世界的に期待されています。私たちの研究グループでは、磁気スキルミオンに関する基礎学理の構築と、応用を見据えた新しいアイディアの創出を目指した研究を続けています。具体的には、磁気スキルミオンの動的性質やメモリ素子としての取り扱いやすさを調べること、また本研究の理論を実現する候補物質の探索などが今後の課題です。
参考文献
“Zero-Field Skyrmions with a High Topological Number in Itinerant Magnets”, R. Ozawa, S. Hayami, and Y. Motome, Phys. Rev. Lett. 118, 147205 (2017).
doi: https://doi.org/10.1103/PhysRevLett.118.147205
この記事を書いた人
- 東京大学大学院 工学系研究科 物理工学専攻 求研究室 博士後期課程3年(2017年3月時)。大阪府出身。東京大学大学院で博士(工学)を取得。研究テーマは、電子のもつスピンと電荷の自由度が結合した系において発現するトポロジカルなスピン配置。大規模な数値シミュレーション技術を適用して研究を行った。2012年度からフォトンサイエンス・リーディング大学院(ALPS)に所属、2015年度から日本学術振興会特別研究員(DC2)。ロスアラモス国立研究所への約半年間(約3カ月間×2回)の海外派遣などを経て、本研究を遂行した。