マクロな「流れ」とミクロな「量子」の関係 – 曲がった空間の幾何学を用いて「流れ」を理解する
水やコーヒーなどの私たちの身近にありふれた「流体」。これらの身近な物質の「流れ」を、現代物理学が到達した極微の視点から眺めるとどのように理解できるのでしょうか。ここでは、幾何学の言葉で「流れ」を理解するという研究について紹介します。
マクロな「流れ」とミクロな「量子」のギャップ
私たちの身近にある物質は、一見するとツルツルした表面を持つように見え、連続的な構造を持っているように感じられます。このような「連続的な記述」を用いる物理理論の最たる例が「流れ」を取り扱う流体力学です。流体力学はコップの中のコーヒーの流れや、航空機の周囲に生じる空気の流れなどの振る舞いを精密に記述します。
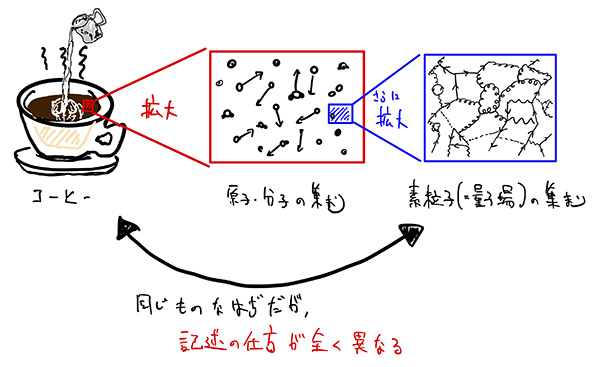
しかし、20世紀に入ってから現代物理学が進展することで、どのような物質も小さな要素に分解していくと、原子や分子といった不連続な「ツブツブ」でできていることがわかりました。そして、さらに小さな(ミクロな)要素に分解していくと、究極的にはクォークや電子と呼ばれる素粒子で構成されていることがわかってきました。現在実験的に検証されている範囲で、実に10-18mという極微の世界の物理法則までが明らかになってきています。このような極微の世界を記述するための理論は量子論(とくに素粒子理論の場合に使われる理論形式は「場の量子論」) と呼ばれており、日常経験とはかけ離れた不思議な現象を予言します。
しかし、すでに見たように、私たちの身近にあるような(素粒子を多数含む)マクロな物質の「流れ」は、流体力学により記述されるのでした。ここに、同じ物質であってもミクロに見たら「量子論」で記述される一方で、マクロに見たら「流体力学」で記述される、という二重性が現れています。このような2つの記述方法のギャップを埋める方法は、はたしてあるのでしょうか?
量子論に基づいて物質の熱的性質を記述する
原子・分子、ひいては素粒子というミクロな記述に基づいて物質のマクロな振る舞いを理解するという、2つの記述の橋渡しを目指す学問(統計力学)は、20世紀初頭にボルツマンという物理学者により始められました。ここで物質のマクロな振る舞いというのは、たとえば「熱を加えたときの物質のあたたまりやすさ」などに代表され、熱的性質と呼ばれます。ボルツマンの研究にとって決定的だったのは、ミクロな記述に基づいて熱的性質を与えるために、「確率的な考え方」を活用するということでした。
さて、ボルツマンの時代にはまだ量子論は構築されていませんでしたが、1950年代の理論の発展により、現在では量子論というミクロな記述に基づいて物質の熱的性質を記述するための方法が明らかになっています。このような理論形式は「虚時間形式の量子論」、あるいはその発展に貢献した日本人(松原 武生博士)の名前をとって「松原形式の量子論」と呼ばれています。詳細の説明は省きますが、この手法では「ある温度の物質を記述するための確率分布」が「量子論において形式的に時間に虚数を代入したときの時間発展」と等価であるということに基づいています。このような理論の発展により、さまざまな物質の熱的性質をミクロな量子論に基づいて理解できるようになったのですが、実はまだ不満な点が残っていたのです。というのも、彼らの理論は「流れ」がすべて止まった後の「静止している流体」に関してしか適用できないのです。つまり、ミルクを入れてかき混ぜている最中のコーヒーや航空機のまわりの空気など、「流れ」が生じている状況は理論の適用範囲外になってしまうのです。
流体力学と重力理論の類似性
さて、これまでに扱えていなかった「流れ」の効果を、量子論に基づいて考慮するためにはどうすればよいのでしょうか。実は大変おもしろいことに、「流れ」の効果は私たちが日常的に感じている重力のアナロジーとして理解することができるので、まずはこのことを見てみましょう。
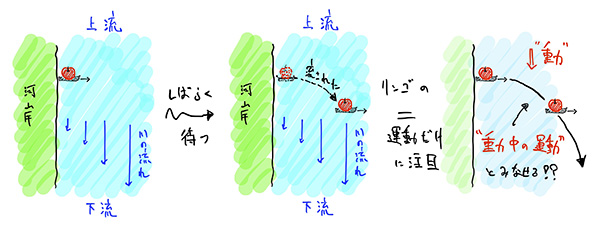
下図にあるように、流れている川の河岸から、一定速度で対岸方向に進む(ラジコンに乗せた)リンゴを出発させてみましょう。しばらく時間が経った後、リンゴは対岸方向に進んではいますが、川の流れによって下流に流されていきます。このごく当たり前の現象を、リンゴの運動のみに注目して見直してみましょう。このように川の流れを見ず、リンゴの運動のみに注目して見てみると、リンゴにはあたかも下流方向への重力を受けて運動したように見えることでしょう。つまり、「流れの効果」というものは、あたかも重力が働いているかのように理解することができるのです。
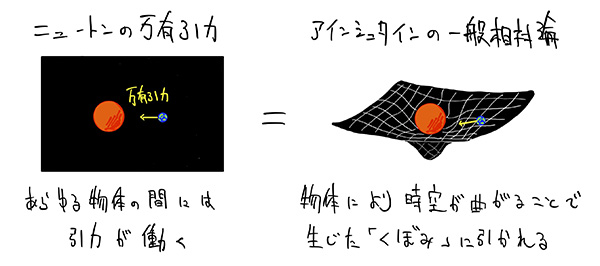
では、重力とは現代物理学ではどのように理解されているのでしょうか。重力を記述する方法として高校で習うのはニュートンの万有引力の法則ですが、現在ではアインシュタインの一般相対性理論によってより正確に記述されることがわかっています。アインシュタインの一般相対性理論では、重力は「曲がった幾何学の効果」として理解されています。つまり、下図のように物体間に直接引力が働くと見るのではなく、物体が空間の中に置かれることで空間が曲がり、その曲がった空間のくぼみに引かれるように物体が運動することで物体に引力が働いているように見える、と理解されています。
「流れ」を幾何学の効果として理解する
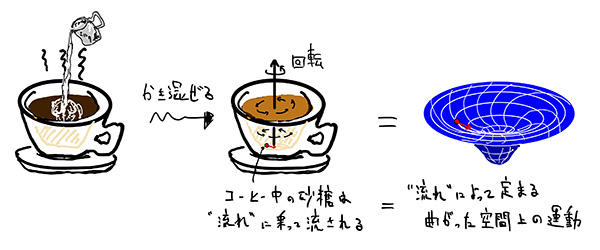
以上の考えを整理しておきましょう。まず、「流れ」の効果は、あたかも重力が働いているものとして理解することができるのでした。そして、現代物理学において重力とは、曲がった空間の幾何学的効果として理解できるということを見ました。これらを組み合わせると「流れの効果を幾何学の効果として理解できるのではないか」という期待が湧きます。今回の研究で私が示したのは、1950年代に定式化されていた虚時間形式の量子論を拡張することで、この期待が実際に成り立っており、「流れ」は曲がった空間中の量子論を考えることで記述できる、というおもしろい事実です。
具体的にこのことを示すためには、「流れ」がない場合についてボルツマンが明らかにしたように、「流れ」が生じている状態を記述する適切な「確率分布」を導入する必要があります。このような局所的に「流れ」が生じている状態を記述する確率分布のひとつとして、「局所ギブス分布」と呼ばれるものが知られています。今回の研究では、この確率分布によって「流れ」が生じている状況を記述すると、その効果が曲がった空間の幾何学的な効果として自然に理解できることわかりました。別の言い方をすると、「流れによって曲がった空間が現れる(創発する)」とも言えます。
以上により重力理論とのアナロジーが正確に成り立っていることがわかったわけですが、さらに嬉しいことに「流れ」の性質を理論的に計算する際にも利点があることもわかりました。一言に「流れ」と言っても、実はエネルギーの流れから運動量の流れ、電荷の流れといったようにさまざまな「流れ」があり、これらは理論的には別々に扱われがちです。しかし、今回の研究では、これらの「流れ」をすべてまとめて、「幾何学的な効果」として理解することができることがわかったのです。
今後の展望:摩擦熱を発する「流れ」の理解に向けて
さて、以上の研究により「流れ」が生じている状況を、量子論に基づいて完全に理解できるようになったと言いたくなります。しかしながら、「流れ」の理解は、実はまだ限られたものにとどまっているのです。その理由は、今回の研究では「散逸的な流れ」と呼ばれるものを取り扱えないからです。「散逸的な流れ」とは、たとえば温度が違う物質をくっつけることで生じる熱の流れのことで、「流れ」とともに摩擦熱を発生させる、不可逆的な現象です。今後、この「散逸的な流れ」も幾何学の言葉で理解できるのかといった点について、研究を行なっていきたいと思います。
参考文献
“Path-integral formula for local thermal equilibrium”, M. Hongo, Annals of Physics, 383, 1 (2017)
「場の量子論と流体力学のつながり」 日高義将, 本郷 優, 数理科学 2017年7月号
この記事を書いた人

- 理化学研究所理論科学連携推進(iTHES)グループの基礎科学特別研究員です。大学院の学生時代から、約2兆度で実現するクォーク・グルーオン・プラズマという極限的な物質状態を「流体」として記述する研究に興味を持ち、「素粒子」と「流体」という全く異なる記述を関係付ける研究を行ってきました。現在は、物質中の電子や宇宙論に対する流体力学の応用や、「乱流」と呼ばれる特別な「流れ」の状態を理解することを目標に研究しています。学部生の頃は高校教員になろうと思っており、教育やサイエンスコミュニケーションにも興味があったので、今回のような解説記事を書くことでも科学研究に貢献していけたらと思っています。