街を行き交う人の傘、水溜りや道路に落ちる雨粒。何気ない日常の風景のなかにも科学では十分解明されていない現象はたくさんあります。特に、固体面に液滴が衝突するような場面は、インクジェット、自動車エンジンのインジェクターやスプレー冷却など数多くの工業分野でも見られ、衝突後の液滴の最大濡れ拡がり面積や液滴形状の安定性は、製品の質や装置の効率を大きく左右する重要な問題です。今回は、そんな“滴”が、平板に衝突したときにどれだけその表面を濡らすことができるのかという疑問に答えることができるかもしれない理論式に関するお話です。

濡れ性とは？

液体が物体表面をどれだけ濡らすことができるのか？　その液体と物体表面間の濡れやすさ（液体の付着しやすさ）を“濡れ性”といいます。一滴の水を物体表面に滴下したときに、べったりと濡れ拡がるのであれば“濡れ性が良い”といいます。このような表面を親水性表面といいます。一方、べったりとは濡れ拡がらず、丸いボールのような状態になる場合、“濡れ性が悪い”といい疎水性表面と表現します。こうした濡れ性の良し悪しは、液体や固体物体を構成する分子の種類や固体表面の粗さにも影響を受けます。特に、空から落ちてくる雨粒のように、運動している物体が静止している固体表面に勢い良く衝突する場合は、その濡れ拡がりの程度は液体内部の流体運動によっても影響を受けます。

シリコンゴム基板上に衝突する純水液滴：それぞれの落下開始地点の高さは、 (a) z=10 mm, (b) z=100 mm, (c) z=700 mm。高さが高いほど（速度が大きい）最大濡れ拡がり面積は大きくなる

何かの現象を科学的に理解するためには、その状態を数学などの手段を用いて数式により表現すると便利です。今、平板の上に液滴が付着している場面を考えます。液体の表面では、その面積をなるだけ小さくしようとする力（表面張力）が働いていますので、固体、気体および液体が接する接触線を起点として、液体表面側に力が働きます（σ1）。固体と気体が接する表面と固体と液体が接する表面側にも表面張力が働くと考えると（厳密ではないのですが）、接触線を中心として、σ2 = σ3 + σ1cosθという関係式を得ます。式中のθは液体表面と固体表面の成す角度を表し、接触角といいます。この式はヤングの式と呼ばれ、1805年にトーマス・ヤングにより提案された接触線での水平方向の力学的なバランス式です。濡れ性の議論をする上では必要不可欠な式として用いられています。

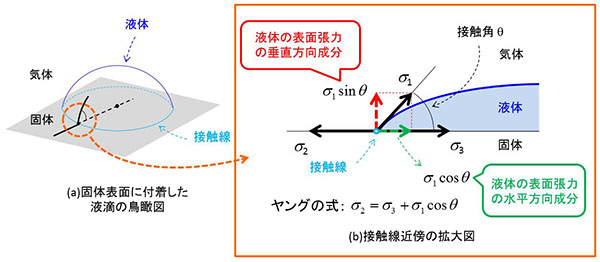
液滴接触線における表面張力の釣り合いに関する概念図：ヤングの式に現れる液体の表面張力の水平方向成分だけでなく、従来無視されてきた垂直方向成分を考慮した理論検討を今回実施した

接触線での垂直方向の表面張力の検討

界面に関する専門書を見ても（たとえばde Gennesら著）接触線での垂直方向の表面張力（σ1sinθ）に関しては、固体表面が変形しない場合は固体の反力と釣り合っているとし、液体と固体間の濡れ性の議論ではほとんど扱われることはありませんでした（特に、固体の表面が変形するような場面は工学上特殊な場合に限られるため）。しかしながら、固体表面上の液滴は固体表面上に単に乗っているのではなく付着しています。つまり、接触線において固体表面を引っ張る力（もしくは引っ張られている）が働いているのです。そのため、たとえ固体表面が変形しなくても作用・反作用の関係によって液体の形状は変形するはずです。つまり、ヤングの式に現れる接触角θは、垂直方向の力も合わせて決まる値ということを意味します。

平板への液滴の衝突現象に関するごく最近までの理論検討では、接触線での水平方向に関する表面張力の影響しか考慮していませんでした。上述の考えに基づき、我々研究グループは、接触線での水平方向だけでなく垂直方向の表面張力の影響を、力としてではなく接触線が移動することで行う仕事（エネルギー）として評価することで理論検討を行いました。通常、力はベクトルとして考えるため、空間を構成する座標軸の各方向成分で分けて考えますが、エネルギーとして考慮することで方向性がなくなり、すべての成分を考慮することになります。また、ここでは詳細な説明を省略しますが、液滴が平板に衝突したあと、液体内部で発生する渦運動により使われるエネルギーの評価方法も見直しました。そのようにして最終的に導かれた新しい理論式は、純水だけでなくエタノール溶液といった液体の種類が異なる場合や固体の種類が異なる場合、さらに幅広い衝突速度にも適用できることがわかりました。

今後の展開

接触線での垂直方向に関する表面張力の影響はヤングの式が提唱されて以来150年以上にもわたり議論が行なわれてきています。そのため、表面張力の垂直方向成分の検討は挑戦的であり、その影響の考慮の是非に関してはさまざまな意見があります。しかしながら、Fernandez-Toledanoらによる分子レベルの数値計算に関する最近の研究では、ヤングの式の水平方向の表面張力の影響だけでなく垂直方向の影響の重要性も証明されていますので、今後の研究の進展に伴い、表面張力の垂直方向成分が本当に重要なのかそうでないのか、その答えが明らかになっていくと考えられます。一方、平板に衝突する滴に関しては、私たちの理論式によってその現象のすべてが明らかにできたわけではありません。平板に衝突した滴は、衝突速度が大きければ平板上で細かい滴に分裂して飛び散ります。このような現象をスプラッシュ現象といいますが、このスプラッシュ現象がどのような条件で生じるのか？ などまだ明確に説明できる理論はありません。このような液滴形状の安定性を解明することが今後の課題です。

 

参考文献
[1] Yonemoto, Y., Kunugi, T, Analytical consideration of liquid droplet impingement on solid surfaces, Sci. Rep., 7, 2362, doi:10.1038/s41598-017-02450-4 (2017).
[2] de Gennes, P. G., Brochard-Wyard, F., Quéré, D., Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves (Springer-Verlag, New York, 2003).
[3] Fernandez-Toledano, J-C., Blake, T. D., De Coninck, J., Young’s equation for a two-liquid system on the nanometer scale, Langmuir, 33, 2929-2938, doi:10.1021/acs.langmuir.7b00267 (2017).

この記事を書いた人

米本幸弘, 功刀資彰
米本幸弘, 功刀資彰
米本幸弘（写真左）
熊本大学大学院先導機構 テニュアトラック助教　
2008年京都大学大学院工学研究科 原子核工学専攻 博士後期課程修了。京都大学・博士（工学）取得。2008年東京理科大学 基礎工学部助教、2010年日本原子力研究開発機構 任期付研究員、2012年原子力安全システム研究所 任期付研究員、2013年より現職。混相流に関する研究に従事し、主に液滴・気泡・濡れ性をキーワードとした表面・界面現象に関する研究を実施している。


功刀資彰（写真右）
京都大学大学院工学研究科 原子核工学専攻 教授
1979年慶応義塾大学工学研究科応用化学専攻修士課程修了。東京大学・博士(工学)取得。1998年東海大学工学部教授、1999年京都大学工学研究科助教授、2007年より現職。混相流における相界面の科学と工学に関する研究、核分裂炉や核融合炉に関する数値流体力学や電磁流体力学に関する研究に従事している。