理科の授業ではじめて微生物をみたとき、我々ヒトなどの哺乳類とは姿・カタチが異なっていて、本当にこの世の生物なのかと感じた記憶があります。実際、彼らの住むミクロの世界では、我々のスケールと異なる物理効果がはたらくため、姿やカタチが異なっているのも不思議ではありません。ドラ○もんのス○ールライトはまだないので、物理の式を解くことで、彼らの世界を体験してみたいと思います。

ミクロの世界で泳いでみる

バクテリアやプランクトン、精子といったミクロの生き物たちのなかには水中を泳ぐものがたくさんいます。彼らの運動を理解するために、周りの水の運動の式を考えてみます。ミクロの世界では液体の粘性の効果がずっと大きくなり、そのため、微小生物の泳ぎはしばしば「ハチミツの中を泳ぐようだ」と例えられます。このような微小世界の流れを表す式はストークス方程式と呼ばれます。

ミクロのホタテは泳げない

さて、液体の粘性の効果が大きいと、少し直感に反することが起こります。それを端的に表しているのが帆立貝定理(scallop theorem)とよばれる、生物運動に対するまわりの液からの制限です。帆立貝は貝殻を開閉することで泳ぐことができますが、このような行きと帰りのカタチが同じ泳ぎ方（往復運動とよばれる）を考えてみましょう。実は、ミクロの世界では往復運動で泳ごうとしても前にも後ろにも進むことができません。もし、ミクロサイズの帆立貝がいたとして、その貝殼を開閉しても泳げないのです。

これは先のストークス方程式が、数式のレベルで、時間反転対称性とよばれる性質を持っていることが原因です。実際の微生物の泳ぎはこの定理が成り立たないように、往復運動でない泳ぎ方をしています。たとえば、精子の尻尾（べん毛）の波が、ウナギの泳ぎのように、頭から後ろの方に一方向に進んでいるのも往復運動でない泳ぎ方です。

ゾウリムシなどに見られる多数の毛（せん毛）を使った波も、往復運動でない泳ぎ方

精子の泳ぎを解いてみる

このように数式を解くことで生き物の運動を理解することができそうです。では、数式を解いた結果と実際の実験観測結果はどれくらい合っているのでしょうか。我々はヒト精子を高速カメラで撮影した顕微鏡映像を使用してその検証を行ってみました。

まず、実際の顕微鏡映像から画像解析を用いてべん毛の形状を取得し、コンピュータ内でべん毛の波形を再構築します。この情報をもとに先のストークス方程式をコンピュータで解いて、コンピュータ内で精子を泳がせてみます。この計算で求まった精子の運動と、実際の顕微鏡の映像を比較したところ、実験的に測定できない部分を考慮すれば、実際の複雑な精子の遊泳軌跡をよく再現していることがわかりました。

方程式を解くことで得られた精子まわりの流れの様子

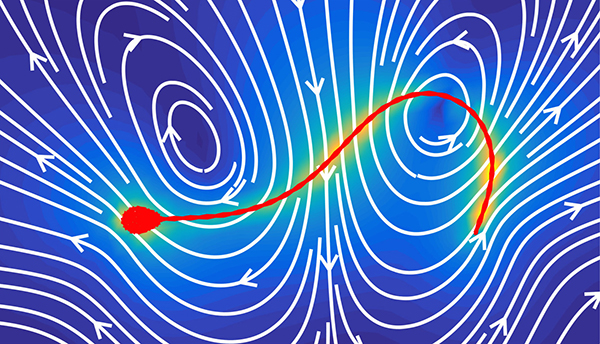
次に同じ方程式から、精子まわりの流れを計算しました。時間的に変化する複雑な流れのなかから、主成分分析とよばれる統計解析を用いることで、中心となっているパターンを抽出してみました。これまで精子まわりには尻尾から押し出されるような流れがあると考えられてきましたが、流れのパターンを抽出すると、実際には単純に押し出しているのではなく、ひねりながら押したり引っ張ったりを繰り返すリズミカルな流れが生じていることがわかりました。

さらに、方程式の性質に注目すると、これらの流れのパターンは、精子が泳ぐ際の力の分布のパターンで表すことが可能であることがわかりました。得られた力の分布は精子の運動を「粗視化」したことに対応し、これにより、精子の運動を比較的単純な数式で表現することができました。

また、今回の研究で得られた「粗視化」された精子の数理モデルを使うことで、卵管内などの狭く複雑な形状内での精子の運動や、多数の精子がいる場合の集団的な運動など、より生体内に近い環境に対しても、数理的アプローチで運動を調べることができると考えています。

精子の旅を覗いてみる

これまで、多くの研究者によって遺伝子やたんぱく質などの分子レベルで受精のメカニズムの研究が行われてきており、毎年新しい発見が報告されています。これらの新しい知見を踏まえ、力学的な視点からの研究が必要なプロセスがまだまだ残っています。

たとえば、顕微鏡下で流れのなかにいる精子が、まるでシャケのように上流にさかのぼって泳ぐ現象（走流性）は100年以上も前から知られていましたが、このメカニズムが、精子の泳ぎと顕微鏡のスライドガラス壁面、そして流れの間の力学的な相互作用によるものだとわかったのは、ほんの最近のことです。精子が卵管内の流れに乗ることで、精子が卵の位置まで誘導されているのではないか、という仮説が注目を集めています。


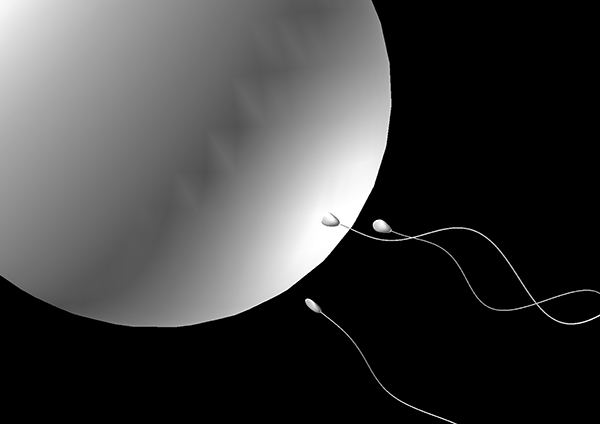
卵に突入しようとする精子の数値シミュレーション

また、卵管内部で精子が泳ぎ方を変化させることが知られており（超活性化とよばれる）、精子が受精能をもつために必要であると考えられています。この超活性化によって、卵に突入する際の精子が生み出す力が2〜3倍に増加することも、数値シミュレーションによってわかってきました。

数理の目で精子の旅を見直すことで、実験観測が難しく理解が進んでいない精子の運動の様子を明らかにできるのではないかと期待しています。また、受精に必要な精子の力学的機能を理解することで、不妊治療の発展に貢献したいと考えています。

参考文献
Ishimoto K, Yamada M. A coordinate-proof of the scallop theorem. SIAM J Appl Math (2012) 72: 1686-1694.
Ishimoto K, Gadêlha, H, Gaffney E A, Smith D J, Kirkman-Brown J. Coarse-graining the flow around a human sperm. Phys Rev Lett (2017) 118: 124501.
Ishimoto K, Gaffney, E A. Fluid flow and sperm guidance: a simulation study of hydrodynamic sperm rheotaxis. J R Soc Interface (2015) 12: 20150172.

この記事を書いた人

石本健太
石本健太
京都大学白眉センター・特定助教。奈良県出身。2015年京都大学大学院理学研究科修了。博士（理学）。同年より現職。京都大学数理解析研究所・特任助教（兼任）。専門は流体力学、特に微小生物の遊泳。最近は受精現象の力学的側面に興味を持っている。