三角形の中心で、数学を学ぶ

三角形は紀元前から研究されている最も基本的な図形です。私たちは、小学校・中学校・高等学校において、三角形の多くの性質を学んできました。しかし、三角形にはまだまだ未知の性質が隠されています。どんなことが未解決なのか、三角形の中心を題材に見ていきましょう。

三角形の重心・内心・Chebyshev心

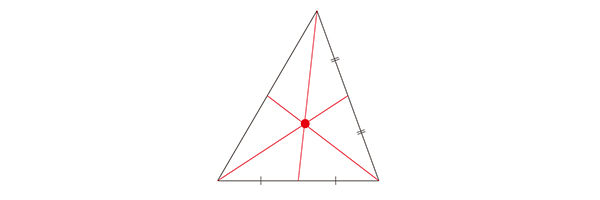
頂点とその対辺の中点を結ぶ線分を中線とよびます。中線たちは1点で交わることが知られています。中線たちの交点を重心とよびます。

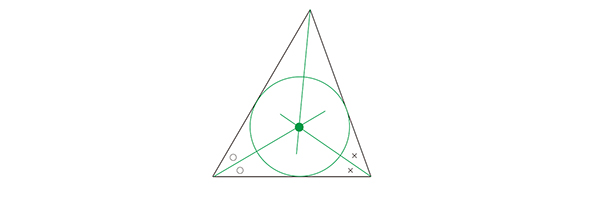
3つの角の二等分線たちは1点で交わることが知られています。角の二等分線たちの交点を内心とよびます。内心は三角形に含まれる最大の円（内接円）の中心になります。

3つの辺の垂直二等分線たちは1点で交わることが知られています。辺の垂直二等分線たちの交点を外心とよびます。外心は三角形の3つの頂点が乗る円（外接円）の中心になります。

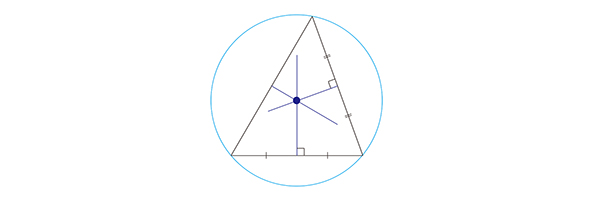
外心には注意が必要です。鈍角三角形を含む最小の円は外接円ではありません。鈍角三角形を含む最小の円は最大辺を直径とする円です。三角形を含む最小の円の中心はChebyshev心とよばれます。

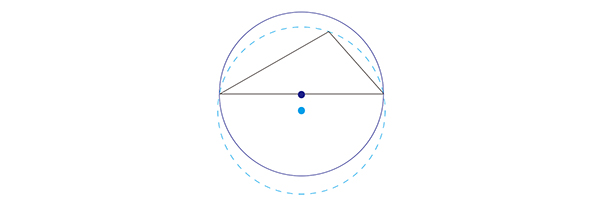
鈍角でない三角形の外心とChebyshev心は一致します。以下、外心ではなくChebyshev心を話に出すことにします。

三角形の公園を明るく照らす点

重心・内心・Chebyshev心以外の三角形の中心を2つ紹介します。まずは、省エネが叫ばれている現代社会に役立ちそうなものを紹介します。

「三角形の公園に街灯を1本立てるとき、どこに街灯を立てたら公園全体の明るさを最大にするか」という問題を考えます。この問題の答えは灯心とよばれています。公園を明るくするには、公園の「真ん中」に街灯を立てた方がよいと思われるので、灯心は三角形の中心と思えます。

灯心の問題を数式で記述する方法について、少しだけ考えます。初めに、公園の「明るさ」とは何かを決めます。ここでは、点の「明るさ」をその点を通る「光の束の密度」としましょう。「点の明るさは光源からの距離の2乗に反比例する」という物理法則を用いると、公園の各点の明るさを式にできます。今は公園全体の明るさを考えたいので、公園の各点の明るさをすべての点で計算して、それらを足し合わせます。これで、公園全体の明るさを式にできました。

公園全体の明るさの式は複雑な形をしているので、灯心を重心・内心・Chebyshev心のようにシンプルに記述することは難しく、未解決です。しかし、どんな三角形の公園にも灯心は1個だけ存在することは証明されています。

三角形の鉄板の一番熱い点

もうひとつ三角形の中心を紹介します。ここでは、熱の伝導と関連するものを紹介します。
三角形の鉄板を熱し、鉄板のどこを触っても温度が100℃になっている状況を考えます。鉄板を熱している熱源のスイッチを切ると、段々と鉄板は冷めていきますが、場所によって冷める速さが異なることを想像できるでしょうか？　実際にやってみてください、と言いたいところですが、火傷の恐れがあるので止めてください。熱源のスイッチを切った後、鉄板の温度は場所によって異なることがわかります。一番熱い点はホットスポットとよばれています。鉄板の「真ん中」ほど熱いと思われるので、ホットスポットは三角形の中心と思えます。

ホットスポットは時間経過とともに動くことが知られています。鉄板の熱は鉄板の乗る平面全体に一様に逃げて行くと仮定すると、ホットスポットは鉄板の内心から重心に向かってひとつの滑らかな曲線を描くことが知られています。しかし、鉄板の熱の逃げ方を別の仮定にすると、ホットスポットの動きを追うことは途端に難しくなり、未解決の問題として残っています。

三角形の心臓

重心・内心・Chebyshev心・灯心・ホットスポットと5つの三角形の中心を紹介しました。灯心は重心・内心・Chebyshev心のようにシンプルに記述できていないと述べました。ホットスポットも同様です。しかし、数学者は諦めの悪い性格をしていて、「ここにある」と言い切れなくても、「この辺りにはある」ということは主張しようとします。そこで、導入されたのが三角形の心臓です。

鈍角でない三角形の心臓は3つの角の二等分線と各辺の垂直二等分線で囲まれた四角形です（下図左）。鋭角でない三角形の心臓は3つの角の二等分線と最大辺の垂直二等分線で囲まれた四角形です（下図右）。

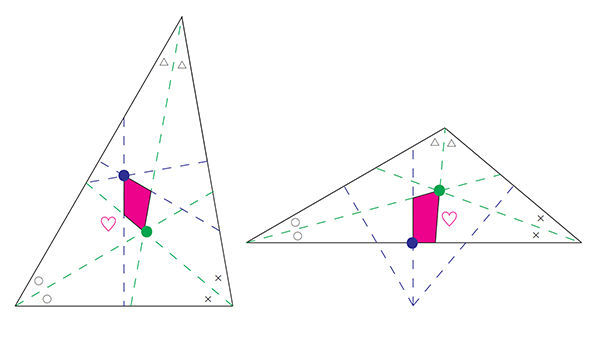
重心・内心・Chebyshev心・灯心・ホットスポットはすべて心臓に含まれることが知られています。特に、内心とChebyshev心は心臓の頂点になっています。

三角形の心臓の大きさがわかれば、中心たちの位置をある程度限定できます。たとえば、二等辺三角形の心臓は頂角の二等分線上に潰れます。よって、正三角形の心臓は1点に潰れて、重心・内心・Chebyshev心・灯心・ホットスポットはすべて一致します。

中心の位置から三角形は決まるか？

三角形が与えられたとき、その中心はどの辺りにあるだろうか？　という疑問には、心臓というひとつの答えが出ました。今度は問題を逆さまにしてみましょう。すなわち、中心の位置がわかっているとき、その三角形はどんな形をしているだろうか？　という問題を考えます。たとえば、「(*)重心・内心・Chebyshev心の少なくとも2つが一致する三角形は正三角形に限る」という定理はこの問題のひとつの答えといえます。

ホットスポットは時間経過とともに動くと述べました。灯心も街灯の高さを変えるに応じて動きます。高さ0の灯心を説明することは難しいですが、高さ無限大の灯心は重心です。

灯心とホットスポットに対して、(*)に似た定理として、「街灯の高さを変えても灯心が動かない三角形は正三角形に限る」と「時間経過してもホットスポットが動かない三角形は正三角形に限る」が知られています。ここで、高さと時刻は実数ですから、街灯の高さを変えることは無限本の街灯を立てること、時間経過を追うことは無限回の観測を行うことに注意します。次に気になるのは、有限本の街灯または有限回の観測で三角形の形状を決定できるか？　ということですが、これは未解決です。

おわりに

三角形は誰もが知る基本的な図形ですが、その中心を見ると興味深い問題が多くあります。それらを理解するには、幾何学だけでなく、解析学も学ぶ必要があり、三角形の中心で数学の世界の広さを知ることができます。

この記事を読んで、数学を勉強したいと思ってくれた人が少しでもいたら幸いです。また、研究のネタを探している大学院生のために入門的参考文献を挙げておきます。

 

参考文献
Rolando Magnanini, An introduction to the study of critical points of solutions of elliptic and parabolic equations, Rend. Instit. Mat. Univ. Trieste 48 (2016), 121–166.
Maria Moszyn’ska, Selected Topics in Convex Geometry, Birkhäuser, Boston, 2006.
Jun O’Hara, Renormalization of potentials and generalized centers, Adv. Appl. Math. 48 (2012), 365–392.