量子化学と機械学習の融合 – 密度汎関数法に基づく深層学習で理論計算の限界に挑む

材料や薬の開発に必要不可欠な物性計算

物理学、化学、生物学の分野において、より良い材料（電池、磁石、半導体、超伝導体、高分子、触媒、太陽光発電など）や病気（がん、エイズ、インフルエンザなど）を治療する新薬の開発は、研究者や技術者にとって常に大きな課題であり続けてきました。特に昨今は、クリーンエネルギーや新型コロナウィルスなどの問題に世界が直面していることで、これらの課題は多くの人々が身近に感じていることでもあると思います。

このような材料や薬の開発においては、物質（分子や結晶）のさまざまな物性を知ることが必要不可欠です。たとえば、物質の最も基本的な物性であるエネルギーや電子密度は、現代のコンピュータシミュレーション技術を用いて、高い精度で計算することができます。

シミュレーションは量子物理学の方程式に基づいており、特にコーン–シャム方程式に基づく密度汎関数法（1998年ノーベル化学賞受賞）が現代で最も使われている理論計算です。理論計算は、第一原理計算あるいは量子化学計算とも呼ばれ、コンピュータとソフトウェアの発展に伴い、今では簡単な物質であればノートパソコンでも数分で実行できるまでになっています。

量子化学計算の問題点と機械学習の活用

量子化学計算は素晴らしい技術ですが、もちろん万能ではなく、主に以下の3つの問題が挙げられると思います。(1) 時間がかかること、(2) 物質を1つひとつ計算しなければならないこと、(3) 計算でわかることには限界があること、です。

特に(3)については、厳密にいえば密度汎関数理論は、基底状態のエネルギーと電子密度を求めることしかできません。しかし、材料や薬を開発するために必要なのは、物質のより高度な機能（たとえば、ある太陽光発電材料の発電効率は何%か、ある薬が新型コロナウィルスにどの程度の効くのか等）を知ることであり、これらは計算だけでわかるようなものではまったくなく、なにもかもシミュレーションできるわけではありません。

これらの問題を解決するために今期待されているのが、大規模データを利活用した人工知能や機械学習の技術です。重要なのは、量子化学計算がすべて機械学習に置き換わるわけではないということです。量子化学計算がなんでもシミュレーションできるわけではないのと同様に、たくさんのデータを人工知能に学習させれば問題がすべて解決するというわけではありません。大切なのは、量子化学と機械学習がそれぞれ、基づいている原理や得意・不得意なことを理解したうえで適切に融合させることであり、それが上記の問題を解決してくれると私たちは考えています。

密度汎関数法の考えに基づく深層学習モデル

ここからは、量子化学と機械学習の融合に関して、私たちの最近の研究を2つ紹介します。

ひとつめの研究では、分子の電子密度を捉える深層学習モデルとして「Quantum deep field (QDF) 」を提案しました。QDFモデルの概略を下図に示します。

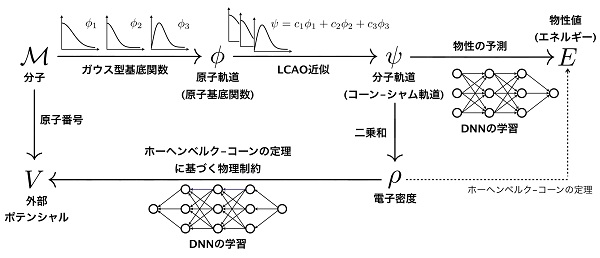
まず分子Mの分子構造（原子座標）を、量子化学計算で用いられる原子の波動関数（厳密にはガウス型の基底関数）Φ（ファイ）に変換し、Φを線形に重ね合わせることで分子の波動関数ψ（プサイ）を得ます。これをLCAO近似（linear combination of atomic orbitals）と呼びます。

次に、ψからエネルギーEを学習するのですが、ここで「ディープニューラルネットワーク（DNN）」を用います。なぜなら、ψからEを得るエネルギー汎関数E=F[ψ]は非常に複雑な形をしており（未だ正確な形はわかっておらず、おそらく一生わからないでしょう）、DNNはこのような非線形関数をデータから学習することを得意としているからです。このように、Φ→ψにおける線形近似を守ったうえで、ψ→Eにおける非線形性を学習するためにDNNを用いるという、量子化学の観点からの適切な分離とモデリングが重要です。

しかし、強い非線形学習手法であるDNNは任意の関数を表現できてしまうため、物理的に意味のないψを無理矢理Eにフィッティングさせてしまう危険があります。つまり、ψ→Eがデータに過学習してしまい、必ずしも物理を学習するわけではないのです。ψに物理的な意味を持たせるために、何らかの対策が必要になってきます。

ここで鍵となるのは、ψから得られる電子密度ρと分子Mから得られるポテンシャルVとが一対一対応するという、密度汎関数理論におけるホーヘンベルグ–コーンの定理です（上図のρ→V）。そして、この対応も非線形なので、DNNを用いて学習することができます。このように、ψ→Eとは逆向きのρ→Vという2つDNNを一緒に学習することで、ψが密度汎関数理論の観点から意味を持ち（これをコーン–シャム軌道といいます）、LCAOにおける波動関数の線形重ね合わせも含め、全体として適切な物理制約を課したうえで物性を学習する深層学習モデルができあがります。

私たちが強調したいのは、QDFモデルにおける1つひとつの計算が量子化学の観点から妥当かつ全体として密度汎関数法の考えに基づくことで、学習モデルが大規模データから物質の本質である波動関数や電子密度を捉えられるという点です。

グラフニューラルネットワークとQDFの予測精度を比較

私たちの最近の研究の2つめは、「グラフニューラルネットワーク（GNN）」についての議論です。GNNは別名、グラフ畳み込みニューラルネットワーク（GCN）あるいはメッセージパッシングニューラルネットワーク（MPNN）とも呼ばれ、近年爆発的に流行し、分子の物性予測に頻繁に用いられるようになりました。

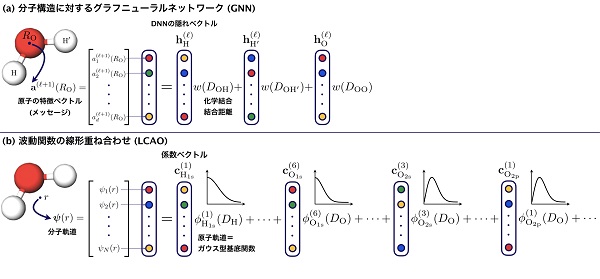
私たちは、GNNが前述のLCAO（波動関数の重ね合わせ）と根本的には同じ計算であることを示しました（下図）。重要な違いは、LCAOは重ね合わせが線形なのに対し、GNNは量子化学の観点から非常に貧弱な波動関数を多層かつ非線形に重ね合わせて学習している点です。多層かつ非線形で大量のパラメータがあれば、もちろん柔軟な波動関数を表現できるかもしれませんが、LCAOと比較してこのように解釈できるGNNは果たして量子化学的に妥当でしょうか？

このようなGNNと、私たちの開発したQDFを比較するために、機械学習モデルの評価方法としては極端な設定を考えました。ベンチマークであるQM9データベースを用いて、14原子以下の小さい分子のエネルギーを1万個学習して、15原子以上の大きい分子のエネルギーを12万個予測しました（下図左）。つまりこれは、外挿予測の評価方法になります。評価の結果、QDFの予測誤差は1〜3 kcal/molであり（下図右）、理論計算のそれが1〜2 kcal/molであることを踏まえると、充分実用に耐えうる精度であるといえます。

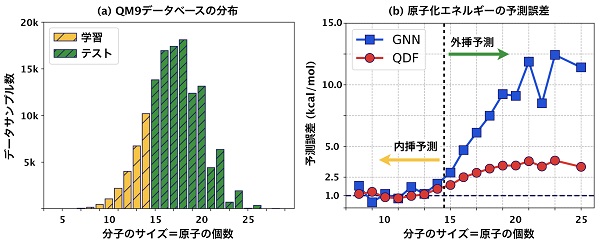
一方でGNNは、内挿精度こそQDFに比べて遜色ないどころか勝っている場合もありますが、外挿精度は著しく悪化します。これは前述のとおり、量子化学に基づかないことが原因であり、内挿精度だけで機械学習モデルの良し悪しを判断すると実用で現場に投入してから大失敗する、なんてことも当然起こりえます。

また、理論計算は1個の分子に数分から数時間かかりますが、QDFは1万個の分子をたった数分で予測できます。つまり、実用に耐えうる外挿精度を保ちながら理論計算を10万倍以上高速化できたことになります。

最後に、ψ→ρで得られた電子密度を可視化した結果を以下に示します。

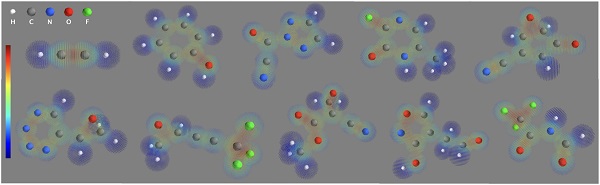
今後の発展へ向けて

このような結果から、先に述べた量子化学計算の問題点のうちの2つ、(1) 時間がかかること、(2) 物質を1つひとつ計算しなければならないこと、はクリアできたと思います。機械学習の大きな利点は、いったん大量のデータ（物質）でモデルを学習してしまえば、その後その学習済みモデルをさまざまな物質の予測に”再利用”できることであり、これにより(2)の問題を回避できます。そして、QDFのような量子化学に基づく外挿性の高い深層学習モデルこそ、(3) 計算でわかることには限界がある、という重要な問題の解決に繋がっていくと私たちは考えています。

私たちは、学習済みモデルを単にまたエネルギーの予測に再利用するだけではなく、そこから”再出発”することができます。つまり、学習済みモデルを用いて、計算ではわからない物質のより高度な機能を、さらに学習して予測することができるのです。

これまで述べてきたように、QDFは量子化学の基本的な情報である波動関数、電子密度、エネルギーなどを適切に考慮したうえで、大規模データを効率的に学習できるモデルとなっています。そして、物質のより高度な機能も元を辿れば、根本的には電子によって説明されます。

しかし、電子→簡単な物性→高度な機能のあいだには大きなギャップがあります。たとえば、電子密度がわかったからといって即座に触媒能がわかるわけではありません。物質科学におけるこのようなギャップを埋めるためには、量子化学の原理に基づきながら、データの利活用を得意とする機械学習を融合させるアプローチが有効であり、私たちはこのような将来を見据えて現在研究を発展させているところです。

本記事で紹介したモデルの実装、使用したデータ、実験結果などはすべて筆者（椿）のGitHubリポジトリ（https://github.com/masashitsubaki/QuantumDeepField_molecule）にて公開しています。また、大規模データで学習済みのモデルも公開していますので、さまざまな研究で自由に使うこともできます。

参考文献
・Masashi Tsubaki and Teruyasu Mizoguchi. “Quantum deep field: Data-driven wave function, electron density generation, and atomization energy prediction and extrapolation with machine learning” Phys. Rev. Lett., 125, 206401, 2020.
DOI: https://doi.org/10.1103/PhysRevLett.125.206401

・Masashi Tsubaki and Teruyasu Mizoguchi. “On the equivalence of molecular graph convolution and molecular wave function with poor basis set” Advances in Neural Information Processing Systems, 33, 2020.