新たな結晶構造である2次元面の「原子層」

結晶構造は、たとえば面心立方格子構造、体心立方格子構造、塩化ナトリウム構造などの3次元構造として広く知られています。近年では、2004年にグラフェンが合成されたことをきっかけとして、さまざまな2次元面の構造を持つ物質が新たに合成され、原子1つ分の厚さの層が重なることで構成される「原子層構造」は、物質の取り得る結晶構造としての地位を得ました。

グラフェンは炭素原子が2次元面上で六角形状の「蜂の巣格子」を組んだ原子層です。また、シリセンやゲルマネンは、シリコン（Si）やゲルマニウム（Ge）の原子層であり、蜂の巣格子が2次元面に垂直な方向に歪んだ形状を持ちます。この他、五角形状の格子を持つ原子層や、異なる原子の組み合わせからなる原子層など、さまざまな構造が知られています。

原子層は合金をつくるか？

周期表には、金（Au）、銀（Ag）、銅（Cu）、アルミニウム（Al）など、放射性元素を除くと40種類以上の金属元素が記載されています。普通の環境下（常温、大気圧）では、その多くは最密充填構造（面心立方や六方最密構造）を安定な構造に持ちます。この最密充填構造は、2次元空間において三角格子構造となるため、金属の原子層構造は三角格子であると予想されます。

適当な2つの金属元素を選び混ぜ合わせると「（2元）合金」が形成されます。2020年に、銅と金の「原子層合金」（CuAu）が実験的に合成され、原子層の研究分野で話題を呼びました。その原子層は、三角格子構造を持つ銅原子層と金原子層を一層ずつ積層させた「歪んだ蜂の巣格子構造」を持っていました。

一般に、銅と金は相性がよく、元素の混合比に依存して複数の結晶構造を持つことが知られています。したがって、CuAuの原子層が合成されたことは、この相性の良さによるものと推測されます。それでは、CuAu以外に原子層合金は存在するのでしょうか？

CuAuの原子層構造の上面図（左）と側面図（右）
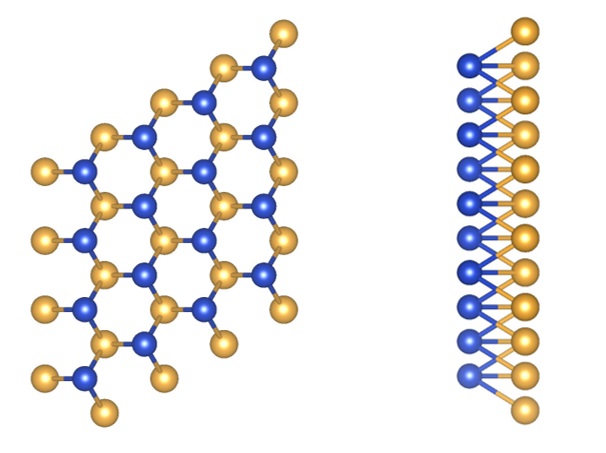
三角格子構造を持つ銅原子層（青）と金原子層（オレンジ）が左右にずれて積層することで、CuAuは歪んだ蜂の巣格子構造を示す。

新物質を網羅探索する「ハイスループット計算」

新物質の存在を予測するには、その物質が「安定か？ 不安定か？」を検証する必要があります。物質の安定性を調べるためには、量子力学に基づく「計算物質科学」の方法を用いて、エネルギー計算や格子振動計算を実行する必要があります。しかし実際的な問題として、研究者が所有する計算機が1台のみの場合、考察対象となる大量の物質群に対してエネルギー計算などを実行することは大変困難です。

周期表より、2元合金の組合せは1000種類程度と見積もられます。また、各々の合金に対してたとえば5種類の結晶構造を考える場合、5000個の候補となる構造があります。ひとつの構造のエネルギー計算に10分の計算時間を要すると仮定すると、総計算時間は50000分 = 833時間 = 34.7日となり、計算を完了するためには膨大な時間が必要です。格子振動計算を網羅的に実行する場合は、さらに10倍以上の時間が必要です。このため前述の疑問に答えるには、たくさんの計算機の集合体であるスーパーコンピュータを用いた「ハイスループット計算」を行う必要があります。

ハイスループット計算は、複数台の計算機を用いて大量の計算データを収集する方法です。計算物質科学の方法を用いると、原子位置と原子の種類のみの情報を用いて物質の電子状態や原子に作用する力を計算し、物質の安定構造を予測することができます。計算機性能の向上に伴い、各々の物質の物性予測に必要な計算時間が短縮しました。このため、複数台の計算機（スーパーコンピュータなど）を用いることで大量の計算ジョブを実行し、膨大な数の物質の物性予測を効率的に行うことができるようになったのです。

ハイスループット計算の概念図
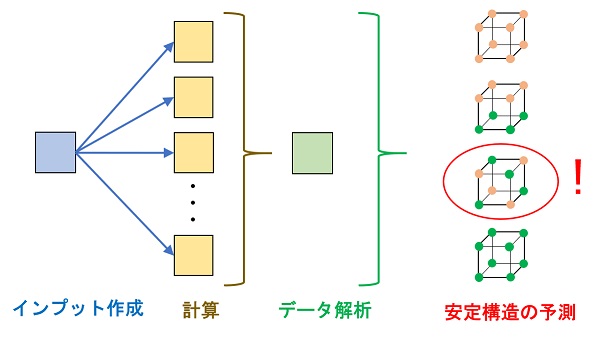
複数台の計算機を用いて同時に計算ジョブを実行することで、大量の計算データを取得する。計算物質科学においては、エネルギーや格子振動の解析を行うことで物質の安定な構造を予測する。

原子層合金のエネルギー計算からわかったこと

本研究では、46種類の金属元素の組合せ1081種類の合金に対してさまざまな結晶構造を考え、東京大学物性研究所や名古屋大学のスーパーコンピュータを利用して、2元合金のエネルギーを網羅的に計算しました。合金の安定性を判断する指標となる「形成エネルギー」という量を計算することで、その安定性を調べました。

その結果、歪んだ蜂の巣格子構造を持つ6個の合金（AlPt, AuBa, AuLi, AuRb, LiPt, LuPt）が負の形成エネルギーを持ち、エネルギー的に安定であることがわかりました。不思議なことに、実験的合成が確認されているAuCuの蜂の巣格子構造は、正値の形成エネルギーが算出され、それゆえ不安定構造であると予測されました。また、負値の形成エネルギーを持つこれらの合金に対して「格子振動計算」を実行し、原子位置の微小変位に対する安定性（動的安定性）も調べたところ、今度は逆に、AlPtとLiPtを除く原子層合金が不安定であることが予測されました。

以上を整理すると、「合金の形成エネルギーが負値であることは、その合金が動的安定性を持つための十分条件でも必要条件でもない」という結論を得ます。合金の安定性に関する計算科学的研究において、形成エネルギーは比較的容易に計算可能です。しかし本研究結果は、このエネルギー値だけで合金の安定性を完全に理解することはできないことを示しています。

2次元と3次元空間での結晶構造の類似性から予測

そこで、合金の形成エネルギーではなく「結晶構造の類似性」に注目し、安定な原子層合金の探索を行いました。2層の原子層からなる歪んだ蜂の巣格子を面に垂直な方向に積層させると「タングステンカーバイド構造」が得られます。そこで「タングステンカーバイド構造が安定に存在するならば、歪んだ蜂の巣格子構造の原子層合金も安定である」と予想し、候補物質の格子振動計算を行いました。

その結果、予想通りのデータが得られ、計41種類の蜂の巣格子構造を持つ原子層合金が安定に存在することを予言しました（15種類のLi合金、その他AlPtなどを含む26種類の合金）。

タングステンカーバイド構造
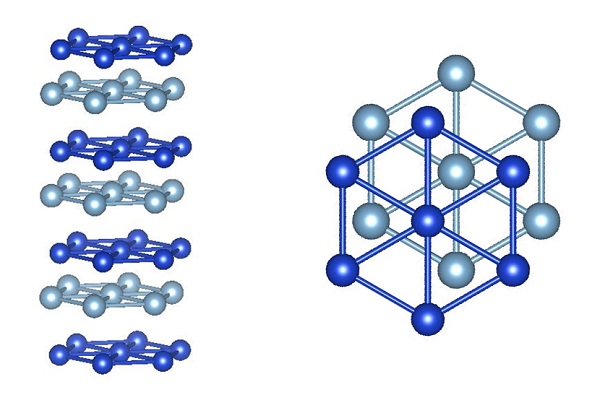
三角格子構造を持つ原子層AとBが左右にずれて交互に積層したような構造、または歪んだ蜂の巣格子構造が積層したような構造を持つ。

結晶構造の類似性に基づく原子層構造の予測方法は、ポロニウムの原子層構造についても応用可能です。ポロニウムは、ポーランドのキュリー夫人が発見したことで有名な放射性元素であり、単純立方格子構造を持つ唯一の単純金属として知られています。単純立方格子と類似する原子層構造は完全に平坦な「正方格子」であり、格子振動計算を行うことによりその構造安定性が確認されました。この原子層は「ポロニウメン」と名付けられています。

今後は本研究によって得た知見に基づき、原子層や合金などの安定性についてさらに理解を深めたいと考えています。本記事タイトルの疑問に答えるには、3次元空間での合金の安定性についても理解を深める必要があるようです。

参考文献

・Shota Ono, Two-dimensional square lattice polonium stabilized by the spin-orbit coupling, Scientific Reports 10, 11810 (2020).
DOI：10.1038/s41598-020-68877-4

・Shota Ono, Dynamical stability of two-dimensional metals in the periodic table, Physical Review B 102, 165424 (2020).
DOI：10.1103/PhysRevB.102.165424

・Shota Ono and Honoka Satomi, High-throughput computational search for two-dimensional binary compounds: Energetic stability versus synthesizability of three-dimensional counterparts, Physical Review B 103, L121403 (2021).
DOI：10.1103/PhysRevB.103.L121403

この記事を書いた人

小野 頌太
小野 頌太
岐阜大学工学部　電気電子・情報工学科　応用物理コース　助教
北海道大学大学院工学研究科修了後、横浜国立大学大学院工学研究院助教、米国カリフォルニア大学バークレー校客員研究員を経て、2016年より現職。
計算科学の手法を用いて、物質の安定性や非平衡電子緩和など「格子振動」が関係する物性を研究しています。