細胞コロニーにみられる「動的スケーリング則」の不思議 – 実験と数理モデルから明らかになったこと
細胞コロニーが一定の構造を形成する仕組み
生命科学者は目的に応じてさまざまな種類の培養細胞を使って実験を行います。その種類はJCRB 細胞バンクに登録されているものだけで1300種余りにも及びます。それぞれの細胞種は固有の性質を持っており、シャーレ上で培養してみると種ごとに異なった形態のコロニーを形成することからも、その一端を伺い知ることができます。
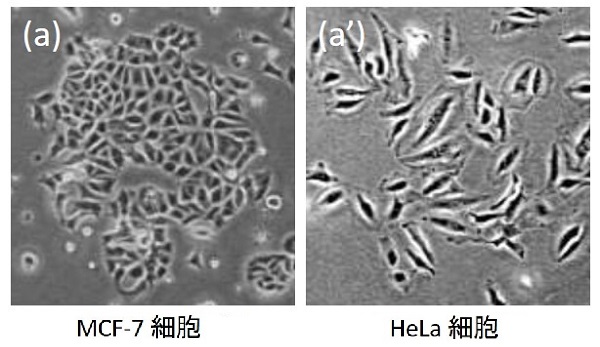
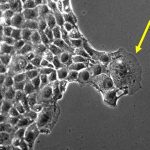
細胞コロニーは細胞種ごとに同じような形態を取る一方、それを構成する細胞の運動、増殖、遺伝子発現などはランダムな振る舞いをすることがわかってきています。では、細胞コロニーはどのような仕組みで一定の構造を形成しているのでしょうか? 実は近年、確率的な効果によって出現する特徴的な空間的・時間的パターンが存在することがわかってきました。それは「動的スケーリング則」と呼ばれるものです。
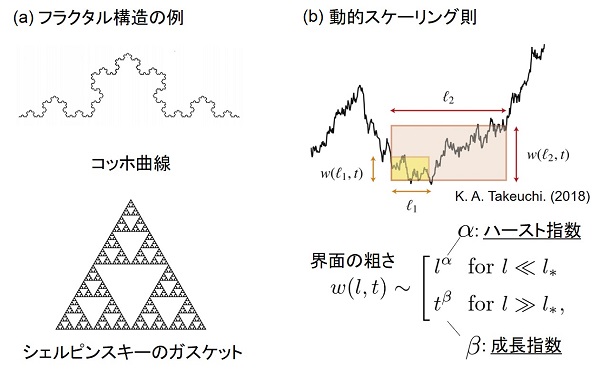
動的スケーリング則とは、界面の「粗さ」を定量したときに、その値が計測する領域の広さと、観察時間との双方に対してべき乗則に従って増加する空間的・時間的な性質をいいます。前者のような計測量と計測する領域の広さがべき乗則に従う性質は「フラクタル」と呼ばれ、代表的な例としてコッホ曲線やシェルピンスキーのガスケットなどが知られています。動的スケーリング則はフラクタルの性質に加えて、観察時間に対してのべき乗則も備わったものと理解することができます。
動的スケーリング則と統計物理学
これまで、動的スケーリング則を示す現象はいくつか報告されてきましたが、それがどのようなメカニズムから生み出されるのか不明な場合が多いという課題がありました。
動的スケーリング則の形成メカニズムについては、これまでに統計物理学の世界でよく研究されており、Edwards-Wilkinson (EW) 方程式や Kardar-Parisi-Zhang (KPZ) 方程式などの生み出すダイナミクスが動的スケーリング則を示すことが知られています。しかし、実験的に観察されている動的スケーリング則と、これらの方程式の結びつきは未だはっきりとはわかっていません。
そこで今回我々は、上皮細胞(MDCK細胞)コロニーの輪郭形状に着目し、MDCK細胞コロニーの界面がどのように拡大していくか実験的に観察することで、動的スケーリング則と統計物理学の方程式との関連を調べました。
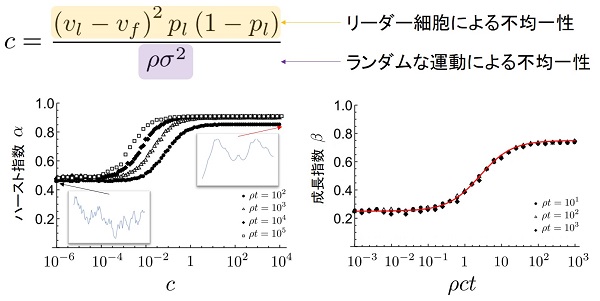
動的スケーリング則は、スケーリング指数と呼ばれる2つの指数により分類されます。ひとつは「ハースト指数」と呼ばれ、界面の粗さの空間相関に対応した指数です。もうひとつは「成長指数」と呼ばれ、界面全体の時間発展に対応した指数です。EW方程式については粉体が重力に従い蓄積して作られる構造と、KPZ方程式については液晶乱流や特殊な環境下でのバクテリアコロニーなどが作り出す構造と同じスケーリング指数を呈することが知られています。
今回観察されたMDCK細胞コロニーの界面の動的スケーリング則は、EW方程式やKPZ方程式が生み出すものと比べて大きいスケーリング指数で特徴づけられることがわかりました。
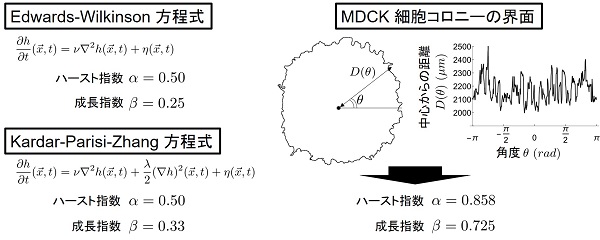
右:今回MDCK細胞コロニーの界面で観察された動的スケーリング則。
細胞コロニーの界面において計測されたスケーリング指数はハースト指数、成長指数共に比較的大きい値を取る。
「リーダー細胞」の振る舞いを数理モデルで表現する
我々は、観察された動的スケーリング則を生み出すメカニズムを明らかにするべく、細胞コロニー界面を形成している辺縁部の細胞がどのような振る舞いをするか観察しました。その結果、細胞集団の中に、サイズが大きく運動性の高い細胞が出現することがわかりました。この細胞は「リーダー細胞」と呼ばれ、細胞の集団運動においてたびたび出現し、周辺の細胞を牽引する重要な役割を担うことが細胞生物学の分野でよく知られています。形態形成や創傷治癒などの生理的な場合に加え、腫瘍の浸潤など疾患の進行にも関与していることが報告されています。
このリーダー細胞の振る舞いが、今回得られた動的スケーリング則の形成に寄与しているのではないかと考え、我々は辺縁部の細胞の運動を表現する数理モデルにリーダー細胞の存在を組み込みました。数理モデルを構築するにあたり、実験的に観察した細胞の振る舞いから(1)辺縁部の細胞はそれぞれ細胞間接着により結びつけられている、(2)リーダー細胞はランダムに出現する、(3)細胞はランダムに運動することを仮定しました。パラメータとしては細胞間接着の強さ、リーダー細胞の割合、細胞の運動性が含まれます。これらの値については観察データから推定した値を用いました。
この数理モデルを用いて数値シミュレーションを行ったところ、細胞コロニーの界面の拡大するスピードや、中心から界面までの距離のヒストグラムなどを再現できるだけではなく、実験的に得られたものとほぼ同じ動的スケーリング則も得られました。
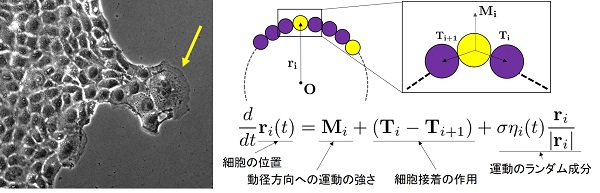
右:構築した数理モデルのスキーム。コロニーの辺縁に位置する細胞が隣接した細胞と相互作用しながら運動することで界面形状が変化していく。
数理モデルの検証と解析
しかしながら、この結果は我々の数理モデルが観察された動的スケーリング則を表現できる、ということに過ぎず、実際にシャーレの中で数理モデルと同じ機構が働いているとは限りません。そこで、シャーレの基質をガラス面からコラーゲンコートしたものに変更して細胞の運動性を増加させて細胞コロニーを観察したところ、この場合についても得られたスケーリング指数は数理モデルによる予測と一致していました。このことは今回仮定したようなメカニズムで「動的スケーリング則」が生まれることを強く示唆します。

加えて、この数理モデルについて解析することで、細胞の運動性や接着の強さなどの物理量とスケーリング指数の関係を導出することができます。数理モデルにより得られる空間パターンに対してのフーリエ変換を考え、パワースペクトルの期待値を導出することで、リーダー細胞により生み出される界面の不均一性と、ランダムな細胞運動により生み出される不均一性の
「つりあい」に応じてスケーリング指数が変化する描像が得られました。
おわりに
以上の結果から、細胞コロニー界面の示す動的スケーリング則はリーダー細胞の特徴的な振る舞いによって生じると考えられます。生体におけるフラクタル構造や動的スケーリング則の生理的な意味については未だにはっきりしていません。しかしながら、このような小さいスケールでの確率的な不均一性を利用し、大きなスケールでの決定論的な構造・機能を作り出すような現象がこの先どんどん明らかになり、同時にそのメカニズムを明らかにする理論的手法は今後ますますおもしろくなっていくのではないか、と期待しながら研究しています。
参考文献
・Takeuchi, K. A. An appetizer to modern developments on the Kardar-Parisi-Zhang universality class. Physica A: Statistical Mechanics and its Applications 504, 77-105 (2018). https://doi.org/10.1016/j.physa.2018.03.009
・Haga, H., Irahara, C., Kobayashi, R., Nakagaki, T. & Kawabata, K. Collective Movement of Epithelial Cells on a Collagen Gel Substrate. Biophysical Journal 88, 2250-2256 (2005). https://doi.org/10.1529/biophysj.104.047654
・Oguma, T., Takigawa-Imamura, H. & Miura, T. Mechanism underlying dynamic scaling properties observed in the contour of spreading epithelial monolayer. Physical Review E 102, 062408 (2020). https://journals.aps.org/pre/abstract/10.1103/PhysRevE.102.062408
この記事を書いた人
-
九州大学医学研究院系統解剖学分野在学中。
確率的な現象と、生物が作り出すパターンの関係について興味を持って研究しています。