量子ランダムウォークは自由に操れるか? – 量子の世界の「コイン」の働き
酔っぱらいの歩行はランダムウォーク
たくさんお酒を飲んだ酔っ払いは、右へ左へとふらふらと千鳥足で歩きます。この酔っ払いは歩き続けたらどのようになるのでしょうか? その結果はコイントスを行い、表が出たら右に、裏が出たら左に1歩移動し、移動した先でこれを繰り返したようなランダムウォークに従います。
しばらくランダムウォークを繰り返したあとにウォーカーがいる場所の確率分布は、出発した地点が高い確率となる分布に従います。つまり、酔っ払いは右に左にランダムに移動しますが、歩き続けても、右に進みすぎたり、左に進みすぎたりすることなく、出発位置付近にいることが多いということです。
ランダムウォークは、酔っぱらいの歩行から、 株価の変動まで、さまざまな不規則性を持つシステムの確率過程モデルとして使われています。コンピュータサイエンスの分野では、ランダムなシステムでの計算アルゴリズムの設計のために使われています。
ミクロな世界でのランダムウォーク
ミクロな世界では、私たちの身の回りの物理現象が従う物理法則(古典力学)は適応することができず、量子力学の法則に従います。それらの物理現象は、粒子のような性質と同時に波のような性質を併せ持ちます(粒子・波動二重性)。また、同時に複数の状態を取る「状態の重ね合わせ」(忍者の分身の術)という不思議な現象が可能になります。
そんな量子の世界でのランダムウォークである「量子ランダムウォーク」では、ランダムウォークと少し様相が異なります。量子ランダムウォークでは、粒子・波動二重性により、ウォーカーが波のように振舞うため、波の性質である重ね合わせや干渉が起きます。それにより、中心位置に高いピークを持つランダムウォークと異なり、確率分布が左右の両端に高い確率を持った分布となります。
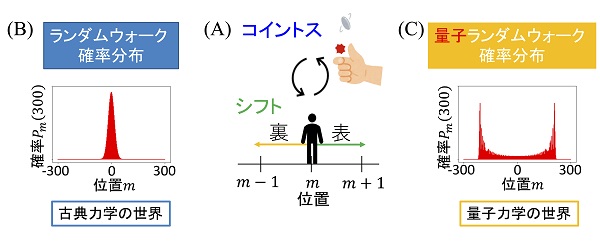
(B)位置0から始めて、300ステップ後にウォーカーがいる位置の確率分布。ランダムウォークの確率分布は、出発位置付近で高い確率を持つ分布に従うことが知られている。
(C)量子ランダムウォークでの300ステップ後にウォーカーがいる位置の確率分布。量子の世界に拡張したランダムウォークでは、量子力学の特徴である重ね合わせや干渉効果によって、左右に高い確率が広がる。
この特性は、幅広いデータ領域での探索を可能にし、新しい探索アルゴリズムとして量子情報科学の分野で発展してきています。また、ランダムウォークが計算アルゴリズムに用いられるのと同様に、量子ランダムウォークも、量子コンピュータ、量子探索問題、量子アルゴリズムなどへの応用が期待されています。量子アルゴリズムの設計においては、情報を任意に操ることが求められています。しかしながら、量子ランダムウォークは本質的にランダム過程であるため、それを制御することは容易ではありませんでした。
量子ランダムウォークにおけるコインの働きとは?
私たちはこれまでに、人工知能の基盤技術である人工ニューロンの研究を行ってきました。その研究を行うなかで、人工ニューロンが構成する人工ニューラルネットワークでの情報の伝達について、興味を持つようになりました。そこで、人工ニューラルネットワークで働くランダムウォークの研究を始めました。本分野においてまったくの素人だった私たちは、量子の世界ではどのようにウォーカーが歩く軌道が決まっているのかという素朴な疑問に至りました。調査をしてみると、ウォーキング・メカニズム、つまり、コインがどんな物理量に対応しているかが、未だに明確でないことがわかりました。
そこで、量子ランダムウォークの制御可能性を追求するために、量子ランダムウォークの動きを決めているコインに着目し、その機能解明のためコインの表と裏が出る確率に時間依存性(時間依存コイン)を導入しました。最初に、コインの働きを理解するために、数値シミュレーションを行い、量子ランダムウォークの軌道(確率分布が高い位置)がコインによってどのように変化するかを見ました。
数値シミュレーションの結果、さまざまな軌道が見られました。当初、時間に依存しないコインを用いたときに得られるような量子ランダムウォークの特徴である左右に広がる軌道のみしか知らなかったため、このように多様な軌道が得られることは予想していませんでした。単にリングが連なっている軌道は、コインの周期性から生成されていることは理解できましたが、リングとラインが交互に現れるような軌道も存在し、その物理的な起源がまったく理解できませんでした。
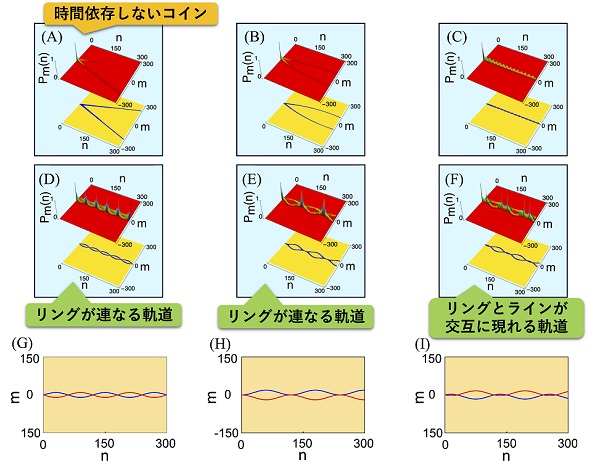
(A)コインの表と裏がでる確率が時間的に変化しない場合は、左右に高い確率が広がり、その軌道は広がっていく。(B)~(F)コインに時間依存性を持たせた場合、さまざまな軌道が見られた。その軌道は、コインの時間依存性の違いによって形が異なる。たとえば、(D)や(E)ではリングが連なっている軌道が見られ、(C)ではリングとラインが交互に現れる軌道が見られる。数値シミュレーションで得られた軌道は、(G)~(I)のように、二つの正弦波によって表されることがわかった。コインのパラメータは正弦波の形や重なり方を変化させる。それによって、さまざまな軌道が生成される。
コインが量子波の速度を制御する
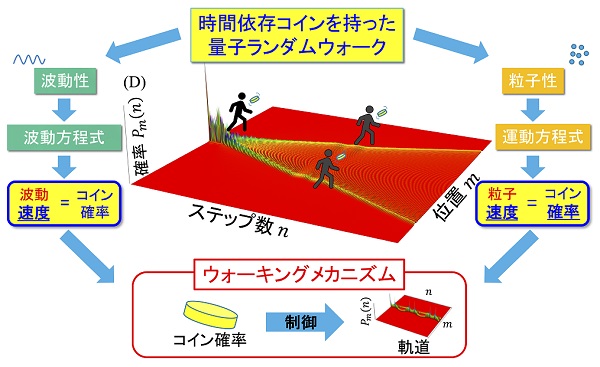
この軌道の起源を探究するため、ウォーカーの波動性・粒子性の両側面から、どのように軌道が制御されているかというウォーキング・メカニズムの解明に取り組みました。コインがウォーカーを左右へ移動させることは確かなのですが、コインがどんな物理量に対応しているかが不明でした。その物理量が何かということが本研究における基本的な問いです。
そこでまず、ウォーカーの波動性に着目しました。ウォーカーの波(量子的波動)とコインとの関わりを明らかにするために、量子ランダムウォークの波動方程式を基に理論解析を行いました。その結果、数値シミュレーションで得られた回帰現象は、量子ランダムウォーク波の速度がコインの表と裏が出る確率の時間変化に依存して出現することが明らかになりました。つまり、これまで波のどんな物理量にコインが対応しているのかが不明でしたが、今回、まったく異なる概念である「コインと波の速度の等価性」を明らかにすることができました。これにより、コインが量子波の速度を制御するというウォーキング・メカニズムを解明することができました。
さらに、量子ランダムウォークのもう一方の量子性である粒子性に着目し、量子ランダムウォーク粒子の力学特性から粒子の速度を求めることで、波動性から求めた結果と同様の結果を得ることができました。この結果を用いると、数値シミュレーションで得られた軌道は、2つの正弦波で表せることがわかりました。さまざまな軌道が見られたのはコインのパラメータの違いによって、2つの正弦波の形や重なり方が違ったからだと理解することができました。
リングとラインが交互に現れる軌道は正弦波同士の重なりが小さいために、交互に大きいリングと小さいリングが現れ、小さいリングがラインに見えていただけだということがわかりました。また、リングが連なる軌道においても、正弦波同士が交わってできる軌道と、正弦波同士が接してできる軌道の2種類があることがわかりました。
最後に、一般的な時間依存性を持つコインに理論を拡張しました。得られたウォーキングメカニズムを用いれば、時間依存コインを適切に設計することで、どんな軌道を持った量子ランダムウォークでも実現可能であることを発見しました。
「量子ランダムウォークがランダムな社会を制する」未来へ
本研究では、量子ランダムウォークがウォーカーの速度を通してコインによって制御されているというウォーキング・メカニズムを明らかにすることに成功しました。ウォーキング・メカニズムを使うことにより、自由自在に軌道をデザインできるため、ランダムな系においても自由に情報を操ことが可能であることがわかりました。この結果は、量子コンピュータや量子ニューラルネットワークなどの次世代の革新的量子情報処理技術において新しい設計指針となります。
現代社会は複雑なネットワーク社会となり、それはますますランダムで複雑化していきます。そのため、ランダムな世界を知り、コントロールできるようになることは重要なことだと考えられます。今回の成果は、ランダムな世界を知る手掛かりになるかもしれません。
今後は、ウォーカーが多数いるシステムにおけるウォーカー同志の相互作用(多体効果)やそれらのあいだの不思議な量子相関(エンタングルメント)の研究へ展開していく予定です。
参考文献
Katayama, H., Hatakenaka, N. & Fujii, T. Floquet-engineered quantum walks. Sci Rep 10, 17544 (2020). https://doi.org/10.1038/s41598-020-74418-w
この記事を書いた人

-
広島大学大学院総合科学研究科 博士課程(前期)に在籍。
広島大学総合科学部在籍中からこれまで量子力学を基盤とする量子情報通信技術に関する理論的研究、特に量子ニューラルネットワークの研究に携わってきました。現在は、量子ニューラルネットワークの研究のみに留まらず、物理学の他の分野に対しても興味と探究心を持っています。
この投稿者の最近の記事
 研究成果2020年11月18日量子ランダムウォークは自由に操れるか? – 量子の世界の「コイン」の働き
研究成果2020年11月18日量子ランダムウォークは自由に操れるか? – 量子の世界の「コイン」の働き



