エネルギー散逸が最小の振り子を開発 – 巨視的物体の量子揺らぎの観測と制御に向けて

量子力学は人間に近いスケールでも成り立っているのか？

原子や電子、光子といった微視的なスケールで観測されるものの振舞いは、量子力学によって説明できます。たとえば、原子を絶対零度まで冷やしたとしても、その動きは静止することなく、原子はゼロ点振動（量子揺らぎ）と呼ばれる振動を伴うことが知られています。これは、原子は粒子であると同時に波としての性質も備えていることから導かれる結論なのですが、微視的スケールではこのような人間の直観とはかけ離れた不思議な現象が数多く観測されています。

我々人間は、微視的なスケールの現象を直接感じ取ることはできませんから、このような不思議な性質を別の世界の出来事のように感じてしまうと思います。しかし、量子力学はあらゆるスケールで成り立つと考えられています。つまり、あなた自身もゼロ点振動をしており、波としての性質も備えていると考えられているのです。ただし、人間的な巨視的スケールにおける量子現象は実際に観測されたことはありません。そこで私は人間ではなく、「大きな振り子」を使って、実験によって巨視的量子現象を観測したいと考えています。

人間的なスケールで量子力学を実証することのみならず、巨視系で量子現象を観測することには深い意義があると考えられます。それは、重力の理解を深めるということです。自然界に存在する基本的な相互作用は4種類あり、量子力学は重力を除いたすべての相互作用を記述することに成功しています。重力は、一般相対論によると、物質によって生じる時空の歪みだと考えられています。そのため、巨視的な物体の量子揺らぎを観測・制御することができれば、量子制御された物体自体が生じる時空の性質（つまり、重力の量子的な性質）を観測することができると考えられます。

たとえば、物体の波としての可干渉性（コヒーレンス）は、重力によって乱される（デコヒーレンスといいます）可能性が理論的に示唆されています。しかし、重力を含んだ完全な量子論が存在しないため、重力によるデコヒーレンスを理論的に予言することは困難であり、実験的な検証が待たれています。

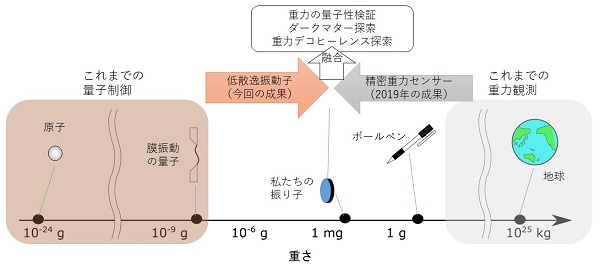
量子を覆い隠す「熱的なデコヒーレンス」

巨視的な振り子のゼロ点振動を検証するためには、どのような実験環境を整えれば良いのでしょうか？ 単純に考えれば、ゼロ点振動の大きさよりも外乱（地面の揺れ、振り子のブラウン運動、音など）による振り子振動を小さくすれば、ゼロ点振動が観測できるはずです。これらの外乱のうち、最も本質的なものはブラウン運動です。

たとえば、空気中に置かれた物体は酸素や窒素原子と衝突することで力（熱的な揺動力）を受けます。酸素や窒素原子の運動を観測しないで振り子の運動だけを観測すると、振り子はランダムな運動をしているように見えます。この運動をブラウン運動と呼びます。巨視的な物体はゼロ点振動より大きなブラウン運動をするので、量子的な波としての干渉性は観測することが困難なのです。これを環境（熱浴ともいいます）との相互作用による「熱的なデコヒーレンス」と呼びます。

ブラウン運動を生じる熱的な揺動力の大きさは、揺動散逸定理と呼ばれる定理から、おおよそ（ボルツマン定数）×（温度）×（エネルギー散逸）×（質量）[N²/Hz]で与えられます（単位にHz^-1が付いていることからわかるように、これは力のパワースペクトル密度です）。この定理から、単純かつ重要な次の事実がわかります。それは、ブラウン運動の影響を抑えるためには、物体の温度を冷やすかエネルギー散逸を小さくすれば良い、ということです。

一般に、ブラウン運動のような熱的な雑音を低減するには、実験環境を低温にすれば良いのですが、そのためのコストは莫大であり、さらに到達可能な温度はそれほど低くありません（本研究の振り子のゼロ点振動振幅は温度換算すれば数十ナノケルビンですが、たとえば希釈冷凍法で到達できる温度は数十ミリケルビンです）。

そこで私は、「エネルギー散逸が究極的に小さな振り子」を利用することで、ゼロ点振動の観測・制御を実現したいと考えています（ブラウン運動などの外乱の他にも、測定の誤差や測定に伴う反作用の影響も考慮に入れなければならないのですが、ここでは割愛します）。

振り子散逸の起源と、低散逸な振り子の条件

2017年、振り子を用いた実験にノーベル物理学賞が授与されました。2つのブラックホールが合体したときに生じた重力波（重力の放射現象で、電磁気力における電磁波に対応します。これらの粒子としての側面をグラビトン、フォトンとそれぞれ呼びます）を、懸架された鏡（振り子）のあいだの距離の変動から観測した成果に対してです。重力波観測においても、本質的な雑音は上述のブラウン運動です。この場合、重力波による振り子の揺れよりもブラウン運動を小さくすれば良いのです。そのためには、やはり振り子のエネルギー散逸を低減すれば良いため、長年のあいだ、重力波分野で振り子の散逸の研究が進められてきました。

振り子振動は、散逸のない重力によるばね（復元力）と、散逸のある懸架線（弦）の復元力の並列ばねのモデル（Zenerモデル）で上手く説明されます。2つのばね定数の実部の比率（∝懸架線の長さ/直径の二次）をQ enhancement factorと呼び、振り子の散逸はこのファクターだけ材料固有の散逸よりも小さくすることが可能です。そのため、散逸の小さな材料を細長く加工して、懸架線として利用します。

散逸源には、thermo-elastic damping、クランプ損失、接着損失などがあります。振り子振動は上部において弦のゆがみを伴うため、弦の中に温度勾配が生じて熱流が生じ、ある緩和時間を持って熱平衡に達します。温度分布の変動は熱膨張を介して弦の機械的な運動をもたらし、この運動は緩和を伴う位相遅れのある振動なので散逸を生じます。これをthermo-elastic dampingと呼び、緩和時間で特徴づけられる周波数特性を持ちます。弦の細線化により、緩和時間を短くすることでこの散逸を抑えることができます。クランプ損失、接着損失に関しては、溶接などで懸架系全体をモノリシックにすることで低減できます。

他にも、振動の高次モード（バイオリン振動など）や内部モード（膜振動など）の影響や弦の表面損失とゆがみの非線形効果、ガスダンピングといった効果を考慮に入れた結果、直径1 μm・長さ5 cmの純シリカ線をシリカ製の鏡に溶接することで、十分に低散逸な振り子が実現できることを理論的に予想しました。

低散逸振り子を開発！ – 量子情報で培われた延伸技術と独自のレーザー溶接を駆使

理論的には、上述のように直径1 μm・長さ5 cmのシリカ線を溶接すれば良いことがわかりましたが、そのような超細長線は世の中に存在しませんでした。そこで、量子情報の分野で広く研究されてきたナノファイバーの作製技術を応用することにしました。

話が少し逸れますが、私は学生時代には重力波望遠鏡の開発に従事していました。その後、量子を対象とした研究を進めるため、東北大学学際科学フロンティア研究所（兼任で電気通信研究所）という異分野融合を目指した研究所に異動しました。そのときたまたま、電気通信研究所の新たな居室の隣の席に、ナノファイバーを開発していたMark Sadgrove准教授（現　東京理科大学准教授）が居たのです！ Mark准教授の研究では、直径100 μm程度のシリカ線を加熱し引っ張ることで、直径約500 nm（長さは1.5 mm程度）に加工しています。この装置を土台とし、超細長線を開発することに成功しました。

しかし、開発当初はシリカ線表面の凸凹が大きいため表面損失が増大し、材料固有の散逸が理論予想よりも一桁大きくなっていました。5 cmの範囲に渡って均一に加工しなければ、散逸を小さくすることができません。そこで、早稲田大学で同様にナノファイバーを用いた研究を進めている青木隆朗教授からアドバイスを頂き、さらに独自に一体型の延伸装置（下図）を開発することで、理論限界程度まで材料固有の散逸を低減することにも成功しました。

開発した超細長線を一体的に鏡に取り付けるため、CO₂レーザーによる溶接システムも独自に開発しました（下図）。

弦と鏡の大きさが著しく異なるため、両物体の溶融する時間スケールには大きな隔たりがあります。この違いに起因して、開発当初、溶接はまったく上手くいきませんでしたが、地道に治具の改良を続けることで溶接ができるようになりました（下図）。

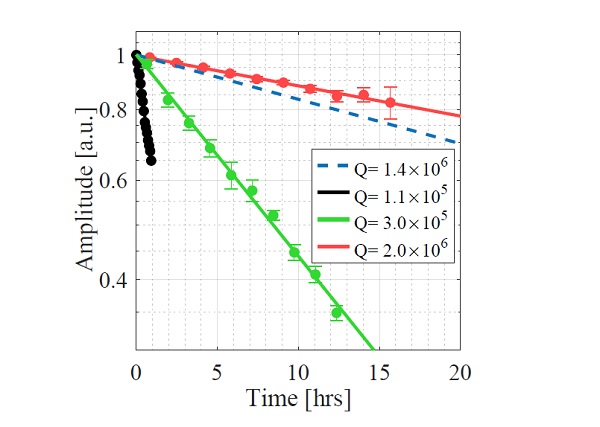
開発した振り子の減衰振動のライフタイム（振幅が1/eになる時間、その逆数がエネルギー散逸）は、下図のように100時間程度にまで向上しました。これにより、ゼロ点振動よりもブラウン運動を小さくし、ゼロ点振動の観測・制御が原理的に可能なことを示せました。

量子振り子が切り開く応用研究

今後5年程度（？）の研究で、量子揺らぎの観測・制御を実現できると考えています。最後に、巨視的量子振り子を開発した後の将来構想についてご紹介します。

振り子の量子揺らぎを観測できるようになれば、観測結果をフィードバックすることで制御することが可能になります。ハイゼンベルクの不確定性原理から、位置と運動量の量子揺らぎの積はプランク定数程度の有限の値を持ちます。つまり、一方を制御によって小さくすれば、他方は大きくなり、スクイーズ状態と呼ばれる状態が生成されます。2組のスクイーズ状態を用意すれば、量子もつれ状態（エンタングルメント）も生成できようになります。量子振り子のあいだの量子もつれの持続時間を詳細に検証すれば、巨視的物体に対する重力の影響も含めた量子デコヒーレンスが直接測定できるようになります。

2012年には、量子デコヒーレンスを実証したSerge Harocheにノーベル賞が授与されましたが、重力を考慮に入れた量子デコヒーレンスが観測できる点において、本研究はその発展型の研究といえるでしょう。量子力学の誕生以降、量子実験の対象は、原子・電子・光子などのアンサンブルから、分子・イオン・固体中の集団励起モード・振動子などを含む個々の系へと広がりをみせてきました。光計測分野における金字塔である重力波望遠鏡の技術を量子制御に応用することで、歴史的な量子実験の巨視化の流れを推し進めることが期待されます。

他にも、量子振り子とダークマターの衝突の観測、重力定数の精密測定への応用、揺らぎの定理の精密検証、計測の量子限界の探索・重力波望遠鏡の次世代技術の開発などが期待されます。つまり、量子振り子は、量子力学・重力理論・天文学・度量衡・非平衡熱力学といった幅広い分野で応用されると考えられます。

参考文献

• Seth B. Catano-Lopez, Jordy G. Santiago-Condori, Keiichi Edamatsu, Nobuyuki Matsumoto, High-Q Milligram-Scale Monolithic Pendulum for Quantum-Limited Gravity Measurements, Physical Review Letters, 124, 221102 (2020)
• Nobuyuki Matsumoto, Seth B. Catano-Lopez, Masakazu Sugawara, Seiya Suzuki, Naofumi Abe, Kentaro Komori, Yuta Michimura, Yoichi Aso, Keiichi Edamatsu, Demonstration of Displacement Sensing of a mg-Scale Pendulum for mm- and mg-Scale Gravity Measurements, Physical Review Letters, 122, 071101 (2019)
• Nobuyuki Matsumoto, Kentaro Komori, Yuta Michimura, Gen Hayase, Yoichi Aso, Kimio Tsubono, 5-mg suspended mirror driven by measurement-induced backaction, Physical Review A, 92, 033825 (2015)