誰も知らなかったグラファイトの姿【後編】 – ファン・デル・ワールス力の新たな理論

誰も知らなかったグラファイトの姿【前編】はこちら

ファン・デル・ワールス力の難しさ

グラファイトは、「グラフェン面が弱いファン・デル・ワールス力で結合してできている物質」であるとして紹介しました。多くの教科書や解説書では、ファン・デル・ワールス力で層状構造が張り合わされて作られる層状物質の典型例として、雲母と並んでグラファイトを紹介しています。これは、もちろん適切な説明ですが、結晶中に現れるファン・デル・ワールス力を議論するときに理論上の注意点があります。そこで、分子間に働く力としてのこの力を復習しておきましょう。

この力は、ファン・デル・ワールスが、従来の理想気体の考え方を超えて、彼の実在気体の理論を完成させるときに、分子間力として概念的に導入したものです。その起源についてはその後に多くの検討が行われました。同じ大きさの正負の電荷を内部にもつ分子は、中性でも電気分極を持っているといえます。電磁気学の法則を用いると、中性の分子において分極があるならば分子間に力が働くことが結論できます。

ところが、分極を持たない中性の分子でも、気体として集団になったときに分子間力が弱く働くことが確認されました。この力はもともと分極がある場合にうまくいく古典電磁気学の方法などだけでは説明が難しいものでした。電場を外部に生じさせない無極性の分子どうしでは、電場がかかったときに生じる誘電分極を考えることもできません。次の誘起分極という考えが必要なのです。

量子力学を用いると、次の効果が表れて良いことがわかります。まず、誘起分極とは、自分だけでは作れないものの相手が近づいてくると自分の中に湧き出てくる分極、と説明できます。このとき、2つの無極性の中性分子間であっても、誘起分極間の相互作用が表れて良いことがわかったのです。この誘起分極を生み出しながら相互作用が起こるというタイプのファン・デル・ワールス力は、ロンドンの分散力と呼ばれます。量子力学という立場で物質が運動すればこそ、湧き出てくる効果が見つかることになります。

分散力を理解するときには、量子力学で定義が明瞭になっている摂動という考え方を用いる説明がよく行われます。そこでは、もともと離れていた分子が、近づいてお互いに相互作用を及ぼし合い始めたとき、結果として全体の力のかかり方がどのように変化するのだろうか、という問いに対して答える方法で、説明が行われます。

これでまでの理論を超えたグラファイト

グラファイトの場合には、離れていたグラフェン面を引き付けるファン・デル・ワールス力によりグラファイトが作られていくところを説明するのであれば、同じ方法が使えます。ところが、結果として安定したグラファイトが形作られた後を考え、その安定状態からの変化で定まる弾性定数を議論するには、摂動という考え方でも説明が難しいことがあります。

まず安定な構造のエネルギーを決める場合には、すべての次数の摂動を計算し尽くすことが求められます。実際、多くの試みがなされていて、現代の計算方法では、十分に精度がある方法が用いられてきた、と考えられていました。安定なグラファイトの平衡格子定数だけであれば、実験値をよく再現する計算手続きは何通りか存在するということができます。

そのひとつが「ACFDT-RPA」と呼ばれる方法です。日本語では、「断熱接続と揺らぎ散逸定理（ACFDT）に基づく乱雑位相近似（RPA）」と訳すことができる理論です。この理論は、ACFDTの段階で電子エネルギーの厳密な表現を用いた正確な理論であるといえます。実際の計算を実行するためには、乱雑位相近似という近似法を追加して用いて全エネルギー計算を可能にすると良いのです。多体系の摂動理論を用いていますので、ファン・デル・ワールス力を表現する能力があります。

グラファイトでいえば、グラフェン面間距離に応じてACFDT-RPA計算を展開基底系の再決定を含めて行うことにより、発生する誘起分極間の相互作用効果が考慮されます。精密なACFDT-RPA計算が適用された結果、2010年には当時の実験的なC₃₃評価値とのよい一致が確認されており、なるほどロンドンの分散力の議論から理解ができると考えられるに至ったことになります。ところが、このときの決定値は、C₃₃ = 36 GPaでした。

計算精度以上に、概念としてのファン・デル・ワールス力がグラファイトの場合に重要である、ということも再考しておくと良いと思います。力がバランスしている安定構造のみを見ているのでは、理論の良し悪しに関する議論が堂々巡りになります。そこで、その周りの変化も順に議論がされてきたという経緯がありました。

今回の測定結果からすると、2つのグラフェン面が離れているときにはファン・デル・ワールス力の表現にとって十分であろうというRPAという高精度近似計算でも、必ずしも安定な状態の周りで十分とは言い切れない可能性が出てきたのです。いずれかの意味で、安定な状態にあるグラファイトでは、ファン・デル・ワールス力についてRPAという近似計算が言い当てている内容を少し超えた理解を必要としていると考えることができます。

新たな理論でグラフェン面の押し戻し効果を再現

ここで、ACFDT-RPAがよい安定平衡状態を導いていることからすると、誘起分極が生じて物質が相互作用を行っているという描像自体は成り立つと考えられます。すると、まず孤立したグラフェンと、グラファイトになってしまった後のグラフェン面で、違いが見つかるはずです。実は、電子の分布自体がかなり変化していることはわかっています。ただし、大きいといってもこの変化は、「強い共有結合」を作るほどに強まったとも言い難いのです。そのため、理論的には、グラフェン面のあいだに強い化学結合が構築されたとまでは結論できないのです。ちょうどその手前にいるのです。

私たちは、ここに安定な位置からグラフェン面が近づくときに押し戻す効果が、グラフェン面が離されるときに引き戻す効果よりも、より強く存在していることに気づきました。より正確には、ACFDT-RPA計算でも捉え切れていない、電子が近い距離に接近するときに発生する「電子相関効果」と呼ばれる効果を、波動関数の変形まで考慮して決めたのです。この補正されたACFDT-RPA+Uという方法と、その近似版でもあるLDA+U+RPA計算によって、弾性定数C₃₃が48 GPa程度まで上昇することがあり得ることを示しました。今回の補正が、多体摂動理論という標準理論に基づいていることは言うまでもありません。

ここで、ものを圧縮したときに押し戻す効果とは、まず原子核間が近づいてしまうことが原因の静電的な斥力効果が主に担っていると考えることができます。電子と電子のあいだの斥力効果の部分も、電子の密度分布から決まるクーロン力により大方は表現できると考えられます。こうした効果をひとつずつ加えていって、全体のエネルギーを決める必要があります。そこには、古典電磁気学の範疇にある説明では把握しきれない、量子力学的な揺らぎ効果、典型的に電子相関効果と呼ばれるエネルギーの部分があります。分散力も、実は電子相関効果の一種であり、引力として効いている部分と考えても良いのです。

まだ決定精度が十分とは言い切れませんが、こうして今回の実験を説明する理論を作り上げることができました。この結果からは、引力部分（長距離電子相関と考えることも、静的相関と考えることもあります）と同時にグラフェン面間を押し戻すこの電子のあいだの量子力学的な相関効果の別の部分（短距離電子相関と考えることも、動的相関と考えることもあります）がバランスして、グラファイトの弾性が決まっているということができるようになってきたといえます。この押し戻し効果の結果、弾性定数C₃₃ は従来理論の予想よりも大きくなるということが今回の理論の立場からの答えです。

グラフェン面間距離dに関するエネルギー変化という見方でいうならば、次のようにもいえます。安定点はエネルギーをdの関数として微分したときに微分がゼロになる点として与えられます。エネルギーのdに関する変化を級数展開することはいつも可能です。そのとき、2次までの展開で十分であるならば調和近似と呼ばれる近似曲線が得られます。実際には、電子と電子の反発からくる波動関数の変形効果にかなり依存して、より高次の非調和項が表れるように見えています。この非調和性の現れ方が、電子相関効果による結論であるといえます。

高配向グラファイトを超えた、真の単結晶グラファイト

今回の実験結果は、これまでの理解に変更を迫ったばかりでなく、真のグラファイトの姿がどのようになっているのかを教えています。まず、測定方法が従来法と大きく異なることはわかっていました。測定データをよく見ると、結晶粒界に相当すると見える部分にレーザー光線が当たっている場合には、予想通り弾性定数C₃₃の局所的な推定値が小さな値になる傾向が見て取れます。そこで試料について改めて考えるために、よく用いられている高配向性熱分解グラファイト（HOPG）を考えてみましょう。

高分解能電子顕微鏡像で、カネカの最新グラファイトと、従来使われているHOPGを、ほぼ同じ程度のスケールで観察した結果を見ると、HOPG（写真からはかなり構造が荒れているように見えますが、このサンプルもグラファイトサンプルとしては相当な高品位のもので、ナノメートルのスケールでは配向性が極めて良い試料です）では、マイクロメートルのスケールで見てしまうと面の向きが揃っているとは言い難いことがわかるでしょう（下図b）。また、この構造から予想されることは、たとえピコ秒レーザー超音波スペクトロスコピー法を用いたとしても、50 GPaに迫る真の弾性定数C₃₃ は見えなかった可能性が高い、ということです。

この高配向グラファイトを超えた真の単結晶グラファイト（下図a）の姿は、弾性定数C₃₃ という物性値によっても明瞭に示されたといえるでしょう。この高い数値をもつ単結晶グラファイトには、さまざまな高い性能が期待されます。今回の数値を標準値として与えることで、より再現性の高い実験が可能になり、安定した物質の合成方法が評価方法と併せて準備することができるようになります。また、製品の質が揃った機能材料をより容易に設計することができるようになる、などの副次的な効果が多数期待できるのです。

グラファイトの熱伝導度

物質の中を伝搬する音波は、その物質全体の構造を反映して敏感に変化が見られるものでもあります。たとえば、超音波診断などの例が示しているように、ものを壊したり傷つけたりせずに、ものの内部を見て取る方法に用いることができます。ピコ秒レーザー超音波スペクトロスコピー法をこうした方法に応用して、物質をセンシングする方法が従来開発されてきました。この応用について、今回のグラファイトが示した高い特性は何をもたらすのでしょうか？

カネカのグラファイトは、弾性の特徴に関連して、「熱伝導度」が極めて高いという特徴があります。これは、グラフェンの面方向に現れる特異的な固さが元になっています。固い物質といえばダイヤモンドでしょう。実は、この炭素の同素体であるダイヤモンドとグラフェンを比較したときに、炭素原子間の距離がより近く強い結合を作っているのが、グラフェンです。そのため、グラフェンの面内方向での各種伝導特性は、物質のなかでも群を抜いて高まることがあるのです。グラフェンを完全な形で積層させているカネカのグラファイトでは、熱伝導特性が必然的に高まっています。では、面間方向ではどのような特徴が表れるのでしょうか？

グラファイトの面間方向は、ファン・デル・ワールス力で結合していると説明してきました。そうであっても、弾性定数C₃₃はシリコン結晶の半分に近いかなり大きな値になるということです。従来、板状グラファイトの面垂直方向の熱伝導度がそれほど高くないことが産業上用いられてきました。今回の結果からは、こうした特性は結晶の不完全性によって表れていた場合が多いとはっきりいえます。

多くのグラファイト様の物質では、グラフェンの並び、配向、さらに積層方向の欠陥、面の欠落、など、多様な構造が中に隠れています。この点を制御すると、音波の伝導という点では問題ない範囲に留めながら、グラフェン面間方向への熱の輸送を抑えてしまう、といった設計すらも可能になってきます。それは、面方向へ熱を積極的に逃がしてしまう設計を行うことで明瞭に可能になっています。

生体センターへの展開

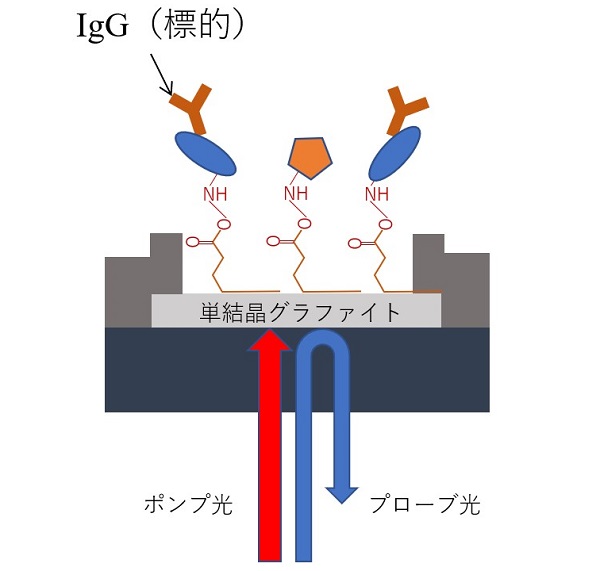
実は、ピコ秒レーザー超音波スペクトロスコピー法を用いた物質センサーを作り上げるときに、大きな応用分野として生体物質センサーを挙げることができるのです。このとき、生体物質を載せる面とは逆の面にレーザーを当てて、物質の重さの変化からくる音波の伝搬の変化を高い感度で観測することができます。ところが、従来用いられる金属薄膜では、レーザー光を連続して照射した際に生じる熱により生体物質ばかりでなくそのセンシング部分、具体的には抗原抗体反応を利用するために用いる抗体が、焼け付いてしまうという課題が残っていました。

今回のグラフェンは、作成時点の調整で、次のことが同時に実現できると期待されます。つまり、非接触で非破壊の条件を壊さずに、抗原抗体反応を利用したウィルスなどのセンサーが実現できます。そこで現在、人々にとっての大きな問題となっているウィルス感染症と、その検査技術にある測定精度・測定時間の課題を、このグラファイトと物質特性の発見からも解決を探る糸口が見つかる可能性があると考えています。

参考文献
K. Kusakabe, A. Wake, A. Nagakubo, K. Murashima, M. Murakami, K. Adachi, and H. Ogi, “Interplanar stiffness in defect-free monocrystalline graphite” Phys. Rev. Materials 4, 043603 (2020). https://doi.org/10.1103/PhysRevMaterials.4.043603