窓の開いた部屋は、開いた系

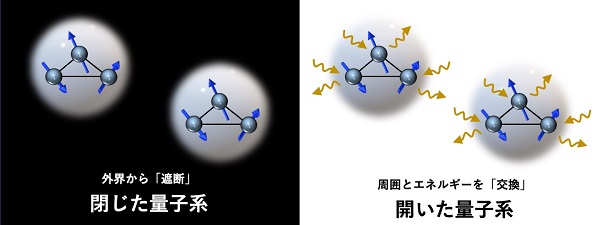
エアコンを使い始めた季節に、部屋の窓をうっかり開けたまま過ごし、思ったほどの心地よさが得られなかった経験はありませんか？ これは、外界とのあいだで空気をやりとりしてしまい、室温の調節が効かなくなってしまうためです。物理学の世界では、「窓の開いた部屋」と「窓の閉じた部屋」の概念を抽象化して、外部との相互作用を通じてエネルギーや粒子が流出入するものを「開いた系」、逆に完全に遮断されたものを「閉じた系」と呼んでいます。

閉じた系と開いた系の違いが顕著に現れるのが、長時間経過した後の「定常状態」です。このことを理解するために、先ほど述べた部屋の温度について考えてみましょう。窓を「閉じた」系では、周りから遮断されることで、エアコンの効いた快適な時間を過ごすことができます。一方で、窓を「開いた」系にしてしまえば、熱や空気が流れ、やがて屋外と変わらない環境になってしまいます。つまり、閉じた系と開いた系の定常状態は、それぞれ異なる温度をもつことになるのです。

ここまでは部屋の温度だけを考えてきましたが、より一般的な自然現象を扱う際にも、外部との相互作用によって、振る舞いが大きく変わる状況が少なくありません。また、窓を閉めていても壁から熱が伝わってしまうように、現実世界において完全な意味での閉じた系は存在しません。したがって、開いた系を正確に理解することが必要となります。

では、開いた量子系とは？

開いた系のなかでも、原子や分子などのミクロな世界を司る量子物理学によって支配されるものは、「開いた量子系」と呼ばれています。何かと難しいイメージのある量子物理学の世界ですが、外部との相互作用を通じたエネルギーの流出入、つまり「散逸」が大切な役割を果たす点においては共通しています。

実は従来、量子物理学者にとって、散逸の存在はあまり嬉しくないものでした。上述した部屋の例と同様に、制御したい対象に望ましくない効果をもたらすことが多かったためです。

それが近年、量子技術の発展により、散逸との付き合い方が少しずつわかってきました。たとえば、量子コンピュータをはじめとする量子デバイスの計算結果を取り出す際には、散逸下での定常状態の違いを測定します。また、実験的に制御された「意図的な」散逸によって、ノイズに対して安定な情報単位（量子ビット）を構築できる、との理論が考案されるなど、さらなる有効活用を研究する動きが加速しています。

外部との相互作用がない「閉じた量子系」と、エネルギーや粒子の流出入のある「開いた量子系」。図中では、それぞれの量子系は原子や量子ビットなどで構成されている。

開いた量子系のシミュレーションは難しい

とはいえ、開いた量子系における散逸の影響について、完全に理解したとは到底いえないのが現状です。量子系の実験におけるエラーの解析や、高精度な量子デバイスを設計するためにも、さらなる研究開発が必要となります。そこで不可欠となるのが、数値シミュレーションです。

しかし、相互作用により多体相関が生まれるような量子の世界では、数値シミュレーションにも大きな困難が伴います。量子状態を記述するために必要なCPUメモリや計算時間が、指数関数的に増えていくためです。地球上で最も性能の優れたスパコンでさえ、厳密にシミュレートできるのは、原子が数十個程度の場合にすぎず、開いた量子系ではさらに半分程度のサイズしか扱えないことが知られています。たとえば分子系などの微視的な輸送デバイスの特性など、数百・数千個のサイズを下らない問題が多く存在することを思えば、気が遠くなりそうな問題です。

そこで工夫を凝らすのが、科学者の仕事です。本研究では、開いた量子系の定常状態を求めるにあたって、ボトルネックである「厳密な」計算を諦める代わりに、計算時間を大幅に圧縮して、近似的に調べるアルゴリズムを新たに提案しました。その中核を担うのが、ニューラルネットワークです。

ニューラルネットワークで定常状態を表す

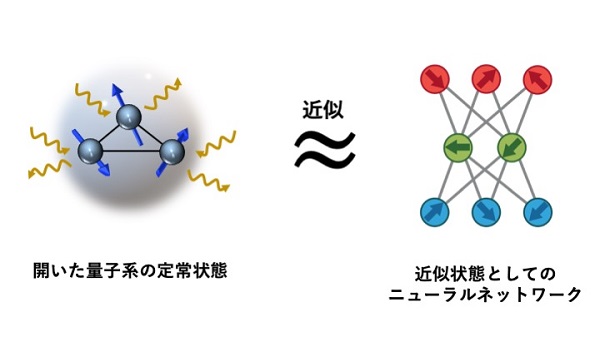
ニューラルネットワークとは、古典的な確率分布や非線形関数を学習するために活用されてきた数理モデルです。学習アルゴリズムをうまく設計することで、計算コストを抑えつつ古典的な確率分布を十分な精度で近似できる場合があることが、機械学習の分野では知られていました。開いた量子系の定常状態は、確率分布を複素振幅1に拡張した形で表現されることから、分布を近似するテクニックと非常に相性が良いのではないか、という発想がアイディアの根幹です。

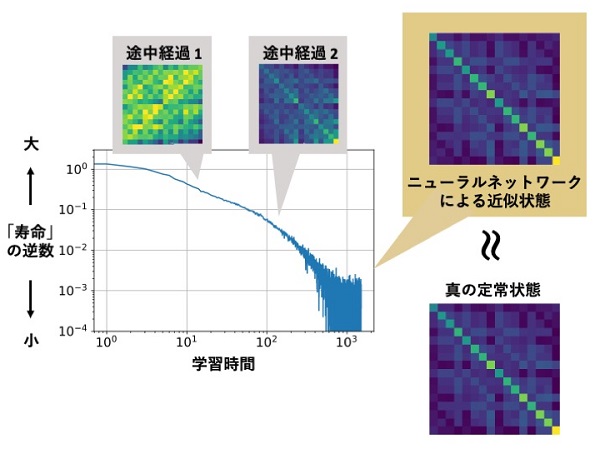
開いた量子系の定常状態に対応する、近似的な「確率分布」としてのニューラルネットワーク。

次に、ニューラルネットワークの学習方法を考えねばなりません。我々のターゲットは定常状態ですが、これは言い方を変えると「寿命が無限大であるような量子状態」です。すなわち、量子状態の寿命が最大化されるようなアルゴリズムを構築してやれば、望む状態が手に入ることになります。

我々の研究では、上のアイディアに基づいた計算を実行すると、実際に定常状態を精度よく近似するニューラルネットワークが得られることを示しました。このとき、学習により得られる定常状態の精度は、学習回数を増やしたり、ニューラルネットワークの構造を複雑化することで、系統的に向上できます。

ニューラルネットワークの学習過程。寿命を最大化するようなアルゴリズムにより、真の定常状態の近似が得られていることがわかる。

今後の発展と展望

本研究では、取り扱いの極めて難しい、開いた量子系の定常状態を、ニューラルネットワークによって近似するアルゴリズムを開発しました。我々が提案したアルゴリズムを用いた場合には、厳密な手法と比べて遥かに多くの原子を取り扱うことが可能となります。これは原子の数に対する計算時間が、厳密に計算した場合には指数関数的に増加するのに対して、我々のアルゴリズムでは多項式的にしか増加しないためです。

背景にあるのは、ニューラルネットワークの表現能力です。深層学習を始めとした計算機科学の分野では、その汎化能力が強力な武器であると認知されていましたが、量子物理の世界においても、量子状態を高精度に表現可能であるという事実には、驚嘆しかありません。量子状態としてのニューラルネットワークは、エンタングルメント2と呼ばれる量子物理学特有の相関を効率的に取り込める、との研究もあり、大きな注目を集め続けています。

機械学習と物理学の融合という、近年急速に発展し続けている分野では、日々新たなアイディアと心踊る研究成果が生まれ続けています。今後もますます多くの手法が開発され、科学的なブレークスルーが起こるのではないかと期待が高まります。

参考文献

  • N. Yoshioka and R. Hamazaki, “Constructing neural stationary states for open quantum many-body systems” Phys. Rev. B 99, 214306 (2019).
    DOI:10.1103/PhysRevB.99.214306.
  • G. Carleo and M. Troyer, “Solving the quantum many-body problem with artificial neural networks” Science 355, 602-606 (2017).
  • D.-L. Deng, X. Li, and S. Das Sarma, “Quantum Entanglement in Neural Network States” Phys. Rev. X 7, 021021 (2017).

脚注
1. 複素振幅に拡張された確率分布：粒子性と波動性をあわせ持つ量子状態の数学的な表現、または波動関数のこと。
2. エンタングルメント：状態の量子的な重ね合わせに起因する、古典物理学では説明のつかない相関のこと。量子もつれとも呼ばれる。

この記事を書いた人

吉岡 信行, 濱崎 立資
吉岡 信行, 濱崎 立資
吉岡 信行（写真左）
2017年より東京大学大学院理学系研究科にて博士課程に所属。2020年日本物理学会若手奨励賞を受賞。専門は物性物理と機械学習の融合領域。量子の世界を見渡すための「望遠鏡」となるような、人間の計算能力を高める技術全般に興味を持っている。
Webサイト：https://sites.google.com/view/nyso/

濱崎 立資（写真右）
2017年より東京大学大学院理学系研究科にて博士課程に所属。日本学術振興会特別研究員(DC1)。専門は統計力学、非平衡物理学。
Webサイト：https://sites.google.com/site/ryusukehamajaki/home