物質の性質は、物質内での原子の種類と並び方で決まる

物質には主に、固体・液体・気体の3つの状態があります。固体には、原子が規則的に配列した「結晶」と、無秩序な「非晶質（アモルファス）」とがあります。さらに、結晶は、物質内全体で原子が規則正しく配列した「単結晶」と、物質内で微小な単結晶が集まった「多結晶」とに分類されます。世の中の多くの固体は、多結晶です。結晶で、何の原子がどこに並んでいるかを「結晶構造」、これを調べることを「結晶構造解析」と言います。

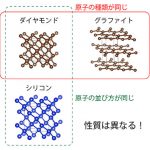
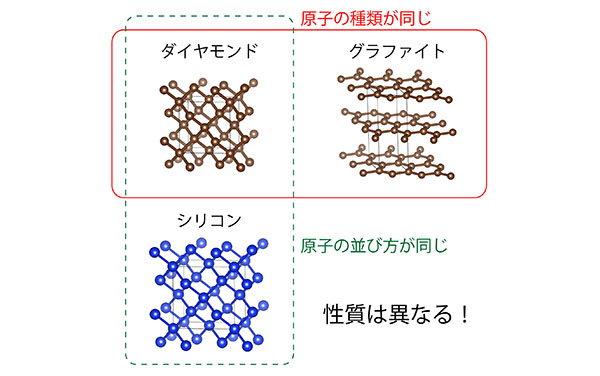
結晶構造解析はとても重要です。たとえば、宝石ダイヤモンドと鉛筆の芯グラファイト（黒鉛）はいずれも炭素原子から構成されていますが、並び方が異なるため性質が異なります。また、ダイヤモンドと半導体シリコンは、原子の並び方は同じですが、種類が異なるため性質が異なります。つまり、物質内での原子の種類と並び方によって、物質の性質が決まっています。そのため、物質の性質を理解したり、より機能的な物質を開発したりするためには、結晶構造解析を正確に行う必要があります。

ダイヤモンド、グラファイト、シリコンの結晶構造

リートベルト解析とその問題点

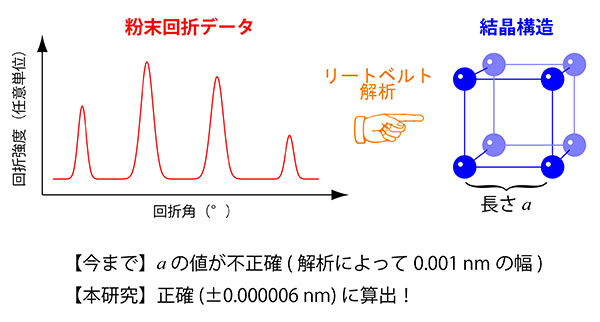
多結晶物質（粉末）の回折データを用いて結晶構造解析を行う手法のひとつに「リートベルト解析」があります。リートベルト解析は、およそ半世紀前にオランダのヒューゴ・リートベルト博士が開発しました。今では、基礎研究はもちろん、ネオジム磁石やリチウムイオン二次電池の電極材料など機能性材料の研究開発や、火星の岩石・イトカワの微粒子の分析、鉄鋼原料やセメント材料の配合比決定、アスベストの評価など、広く用いられています。

しかし、値を正確に知ることができないという問題がありました。同一データでさえ、解析者や解析日、解析に用いるデータ範囲によって算出値が異なります。たとえば、1992年のロデリック・ヒル博士の報告によると、専門家たちの解析結果では、格子定数が0.001 nm（または0.1%）程度の幅をもって互いに異なる値が得られています。測定日や装置の異なる回折データでも同様です。この幅は、温度や圧力、組成比によって生じる伸び縮みや差異と比べて2桁大きいため、とても重大な問題です。つまり、温度等で生じる変化よりも雑な値しか得られません。そのため、特に格子定数を正確に算出する場合は、高価な標準参照試料を試料に混合して測定・解析を行う必要がある、と考えられていました。

リートベルト解析のイメージ図。粉末試料の回折データを測定し、結晶構造を明らかにする解析手法

カギはピーク位置シフト

本研究では、ピーク位置シフトΔ2θに着目しました。ピーク位置シフトとは、どんなに精密な実験をしても必ず伴う、理想の回折ピーク位置からのずれで、測定データが横方向にずれます。Δ2θの成分には、ダイレクトビームのずれ、試料表面位置のずれ、X線が試料を透過することによるずれ、の3つがあります。

正しい格子定数がわかっている標準参照試料 ランタン硼化物LaB6について複数のリートベルト解析を行い、算出された格子定数とΔ2θとの関係を調べたところ、格子定数が正しい場合はΔ2θが妥当なふるまい、格子定数が間違っている場合はΔ2θがあり得ないふるまい、になっていることが確認できました。

次に、複数ある間違った格子定数およびΔ2θが、正しい格子定数およびΔ2θとどのような関係になっているかを、収束指標と合わせて調べたところ、正しい格子定数が算出されている場合、収束指標は最小ではないこと、間違った格子定数は正しい格子定数に比例していること、そのときの比例定数を用いれば間違ったΔ2θをとても良く再現できることがわかりました。

結局、正しいΔ2θは、上記3つの項からなる「実験上存在するピーク位置シフトΔ2θexp」と比例定数の項からなる「解析上現れるピーク位置シフトΔ2θana」を足し合わせたものであり、Δ2θanaが収束指標に影響を与えていることがわかりました。Δ2θanaは今回初めて見出されたもので、正しい解が得られている場合にはゼロになるべきものです。

ところで、LaB6は立方晶系ですので、複数の解析結果同士が比例関係になるのは当たり前でもあります。そこで他の結晶系についても調べたところ、複数の解析結果の格子定数は確かにお互いに比例関係になっていました。加えて、一部の結果についてΔ2θを検証したところ、あり得ない結果（たとえば粉末の充填率が負）になっていることもわかりました。

以上のように、「収束指標を最小にする」という従来の収束基準だけでは、正しい格子定数の相似形しか得られないことが確認できました。正しい格子定数を算出するために、追加指標を提案しています。Δ2θが発散しないことを条件にすることで、Δ2θanaをなるべくゼロにする性質の指標です。追加指標を用いれば、誰でもとても正確(+/– 0.000006 nm)に格子定数を算出できます。従来と比べて2桁以上もの劇的な向上です。標準参照試料を混合する必要もありません。

今回の研究を進めるうえでは、以下2点の工夫をしました。

1点目はすでに述べた「ピーク位置シフト」に注目したことです。というのが、結晶構造解析で回折データから抽出したい情報は、結晶に関するもの（格子定数、分率座標、占有率など）です。ピーク位置シフトは、いわば「ついでに得られる情報」であり、注目されていない（少なくとも論文等でほとんど報告されていない）ことに気がつきました。そこで、「ついでに得られる情報」の妥当性を評価すれば、新たな知見が得られるかもしれないと考えました。

もう1点は、「間違った解をわざと算出」したことです。通常、解析では、正しい解を得ることを目標とするのが当然なのは言うまでもありません。しかし、上記の通り、解析ごとに解が幅をもっていることはわかっており、かつ、どれが正しい解なのかがわからない以上、どこをどのように改良するかの見当がつきません。一方、間違った解であることがわかっていれば、改良点がわかるかもしれないと考えました。

「ついでに得られる情報」に拘った人、わざと間違った解を算出する人に出会ったことはありません。今まで誰もしなかったことをしたことが、本研究の成果に結びついたのだろうと思っています。

おわりに

本研究の成果を例えると、視力が悪い人がメガネをかけて、モノがはっきり見えるようになったようなものです。今までは区別できなかった差・気が付かなかった違いを明確に判断できるようになります。今後、基礎研究における新たな発見はもちろん、新素材の開発や工業製造品の品質管理への活用が期待されます。

参考文献

  • Masami Tsubota, Jiro Kitagawa, “A necessary criterion for obtaining accurate lattice parameters by Rietveld method”, Scientific Reports. 7, 15381 (2017), DOI: 10.1038/s41598-017-15766-y
  • Masami Tsubota, Biswajit Paik, Jiro Kitagawa, “Inter-comparison of lattice parameters and evaluation of peak-shift obtained by Rietveld refinements”, Results in Physics. 15, 102640 (2019), DOI: 10.1016/j.rinp.2019.102640

この記事を書いた人

坪田雅己, 北川二郎
坪田雅己
広島大学理学部物性学科卒業。広島大学大学院先端物質科学研究科博士課程後期修了。日本原子力研究開発機構/SPring-8、広島大学先進機能物質研究センター、高エネルギー加速器研究機構/J-PARCに従事した後、株式会社フィゾニットを設立。著書に、『RIETAN-FPで学ぶリートベルト解析』（情報機構）。固体物性全般に興味があります。

北川二郎
1970年、大阪府生まれ。1993年3月京都大学卒業。1998年3月東京大学大学院理学系研究科博士課程修了。2002年広島大学大学院先端物質科学研究科助手。2012年福岡工業大学工学部准教授、2015年同教授となり、現在に至る。磁性・超伝導材料において、新物質開発を行っている。最近は、化学的な方法による磁性制御や、微細構造と超伝導状態の関係について研究している。また、高エントロピー合金概念を磁性・超伝導材料に適用する研究も始めている。