原子核の「かたち」はまんまるではない？ – あらゆる原子核の”理論計算核データ”を公開
物質の分解と組立
子供のとき、ドライバーを手に、時計をバラバラにして壊してしまい親に叱られた、そんな経験をお持ちの方も多いと思います。しかし、大人である我々も同じことをやっています。物質を細かく分解していったら最後は何になるんだろう？ という疑問を、人類は紀元前の遥か昔から追い求めてきました。
やがて原子という単位に至り、20世紀に入ると、その原子が電子と原子核から構成されていることを知ります。さらに、原子核は陽子と中性子の集合体であり、その陽子と中性子もクォークとグルーオンが結合したものだと考えられています。そして、物質を細かく分解することで、それまで知られていなかった自然法則を発見し、新しい理論を構築してきました。
親はなぜ時計を分解した子供を叱るのでしょう？ それは、バラバラにした部品から時計を組み立てて再び動かすことが難しいからです。発見した物理の法則・理論に従って、クォーク・グルーオンから陽子・中性子を、陽子・中性子から原子核を、原子核・電子から原子・分子・物質がどのように作られているのかを知ることは、バラバラにするよりも難しい問題です。さらに、生命や我々の意識の起源が何なのかを知ることはもっと難しいでしょう。
超ミクロ物体の原子核ってどんな姿？
今回お話する研究の話は、上で述べた「組立」のなかの、陽子と中性子から原子核を作る話です。元素は原子核で決まるので、実際に実験室でこれをやれば、「錬金術」ということになりますが、残念ながら理論計算のお話で、コンピュータの中に作り出します。
我々の身の回りにある物質に含まれている原子核は、大きさ（直径）がおよそ1兆分の1cmの物体です。原子の1万分の1という超ミクロ物体ですが、ここに物質の質量（重さ）のほぼすべてが集中しています。ダイエットで体重を軽くするということは、体の中の原子核（主に酸素・炭素・水素の原子核）の数を減らしているのです。
こんなミクロの世界を記述する理論が量子力学という理論です。量子力学の基礎原理である「不確定性原理」によれば、こんな小さな領域に閉じ込められた陽子や中性子は、静止することができず、激しく運動することが運命付けられています。古典力学では、陽子と中性子が原子核の中で静止して結合した状態を想像してしまいますが、これは「量子の世界」では許されないのです。
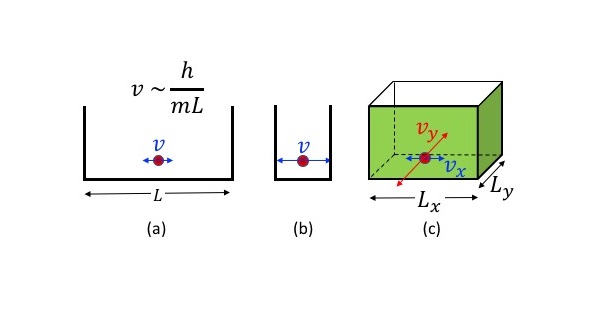
ミクロな世界では、箱に閉じ込められた粒子は完全に静止することができず、フラフラと運動している。粒子の速度は箱の大きさに反比例するため、箱が小さいほど運動は速くなる（(a) < (b)）。また、(c) のように、\(x\) 方向と \(y\) 方向の大きさが異なる2次元（\(L_x\) > \(L_y\)）の箱の場合には、短い方向の速度が大きくなる（\(v_x\) < \(v_y\)）。
原子核の「かたち」はまんまるではない？
原子核の中で陽子・中性子が激しく動いているので、その運動エネルギーは莫大な大きさです。これには、陽子・中性子が従う「パウリ排他律」も関与しています。パウリ排他律とは、ひとつの状態に2つ以上の同種粒子を入れることができないというルールです。
原子核に多くの陽子（中性子）があると、運動エネルギーの小さな状態がすでに他の陽子（中性子）で占有されているため、より大きな速度と運動エネルギーを持たざるを得ないのです。
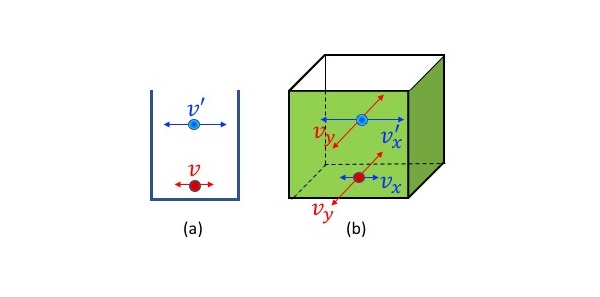
(a) 2個目の粒子は1個目の粒子と同じ状態にはなれないため、1個目より大きな速度 \(v’\) を持つことになる。(b) 多次元の場合は、どれか1方向（図では \(x\) 方向）の速度を1個目より大きくする必要がある（\(v_x\) < \(v_x’\)）。
原子核は、不確定性原理とパウリ排他律に則しながら、この運動エネルギーをできるだけ小さくしようとして、結果的に等方的な速度分布を持ちます。この等方的な速度分布に歪みを与えるとエネルギーを著しく損するため、陽子と中性子の速度分布は「まんまる」なのです。
一方で、原子核の密度分布は必ずしも球形ではなく、さまざまな「かたち」を持つ原子核が出現します。空間的な「かたち」を球形から歪ませることで、エネルギーをむしろ下げることができるのです。どうしてそうなるのか、簡単な例で説明します。
実際の原子核には陽子と中性子がありますが、簡単のため陽子だけで考えることにします。原子核を陽子の小さな入れ物と考えます。体積の決まった空の入れ物に陽子をひとつ入れてみましょう。運動エネルギーを小さくするには、速度分布を等方的にした方が良いので、どの方向にも同じ大きさを持つ「かたち」、すなわち球形の箱がベストです。
不確定性原理によれば、陽子は
すべての方向で、
程度の運動量を持つ状態になります（プランク定数 
、球の直径 
）。しかし、陽子をもうひとつ加えると状況が変わります。パウリ排他律によって次の陽子は同じ状態に入れないので、の3方向のうち、どれかひとつの方向について運動量（速度）を大きくする必要があります。
たとえば、
方向を選んだとしましょう。すると、方向の速度が、
方向よりも大きくなり、異方的な速度分布を持ちます。これはエネルギー的に大きな損です。これが球形ではない「かたち」の“もと”です。原子核は、「かたち」を球形から歪ませることで、速度分布を「まんまる」（等方的）に戻すのです。
再び量子力学の不確定性原理を使います。原子核（入れ物）の方向の大きさを、方向の大きさよりも大きくすれば、方向の運動量を、方向の運動量よりも小さくできます。すると、2個目の陽子が方向に大きな運動量を持っていても、全体として速度分布が等方的になるように、歪みの大きさを調整することができるでしょう。
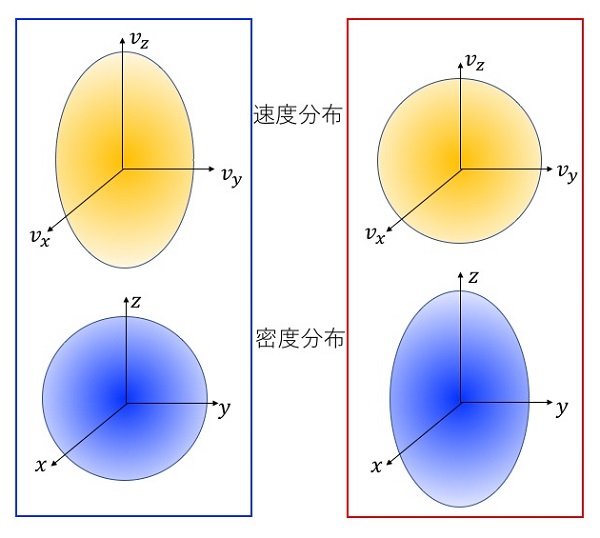
こうして、量子力学の法則に従いながら、原子核は自らその「かたち」を自動的に調整してエネルギーを下げるのです。現実には、原子核は陽子だけでなく中性子も存在し、さらに陽子や中性子には「スピン」という自由度もあるため、ここでの議論はもう少し複雑になりますが、その本質は変わりません。しかし、スピン（スピン・軌道力）の存在は、下図に示すような瓢箪形の不思議なかたちの原子核を生み出すことがあります。
かたちの核図表と理論計算核データ
筑波大学・計算科学研究センター・原子核物理研究部門では、密度汎関数理論と呼ばれる量子多体系を記述する理論とスーパーコンピュータを利用して、これまでに実験で存在が確認されている原子核だけでなく、未知の核種も加えて系統的に計算を行い、原子核がどんな「かたち」をしているのかを解明しました。
また、「かたち」だけでなく、質量や半径、陽子や中性子を剥ぎ取って別の原子核に変換（核変換）するために必要なエネルギーなど、原子核物理学だけでなくさまざまな応用のために有益な情報をWeb上に公開しました。この公開したサイトを、InPACS（Interactive Plot for Atomic nuclei and Computed Shapes）と名付けました。計算で得られた「かたち」で色分けし、好きな核種の「かたち」を図示されることができます。
InPACSで公開しているデータの多くは、ImPACT藤田プログラムの支援を受けて取得したものです。このプロジェクトでは、基礎科学と応用工学に関わる研究者が共同で、原子炉から排出される高レベル放射性廃棄物の低減・資源化に向けた研究開発を行ってきました。放射性廃棄物問題は、原子力発電の継続・廃止に関わらず、人類が直面する世界的な大問題であり、InPACSにおける理論計算核データがこの解決のための一助になることを期待しています。
この記事を書いた人
-
筑波大学・計算科学研究センターおよび数理物質化学研究科・教授。
京都大学大学院物理学第二専攻修士・博士課程修了。博士（理学）。カナダ・チョークリバー研究所、英国・マンチェスター工科大学、理化学研究所などでのポスドク研究員、東北大学・助教、筑波大学・講師、理化学研究所・准主任研究員を経て、2014年より現職。専門は理論核物理。現在、スパコンなどの大規模数値計算による核構造・核反応機構の解明、中性子星の構造などの研究に従事。
