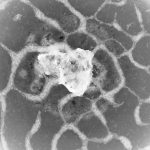
動物はどのように秩序だった群れをつくるのか？ – アクティブマターの物理で迫る、線虫の群れ形成メカニズム

「アクティブマターの物理」とは？

水族館のイワシの群れが秩序だって美しく泳ぐ様子を、みなさんはご覧になったことがあるでしょうか？ 夕暮れどきに飛ぶ鳥の群れは、バードウォッチャーにとって絶好のシャッターチャンスです。イワシや鳥は誰かに指示されているわけでもないのに、なぜ動く方向を揃えてかたまりを作りながら、あちこち移動できるのでしょうか？ これはよく考えても答えが出ない不思議な現象です。

分子がたくさん集まったときに何が起こるかは、統計物理学という分野で深く研究されてきました。統計物理学の手法などを用いながら、生物のように自ら移動する物体が集まったときに起こる現象を研究する「アクティブマターの物理」という新しい学問分野があります。

アクティブマターの物理は、タマス・ビチェックによる数理モデルの提案がひとつの契機となって盛んに研究されるようになり、「生物でも非生物でも、自発的に運動していれば共通するメカニズムで秩序構造が形成される」と予想されています。これまで、非生物の分子や微生物などを利用した研究により、アクティブマターの物理が現実をよく記述できることがわかってきました。

しかしながら、最も高等な生物である動物に対して同様の枠組みを用いることができるかどうかは不透明なままです。なぜなら、野外の魚や鳥などの動物の群れは研究対象として操作するには大きすぎるため、実験室スケールのさまざまな状況下で解析することが一般的には難しいからです。

究極のモデル生物「線虫C.エレガンス」による群れ形成の発見

線虫C. エレガンスは、1960年代に研究に利用され始めた線形動物のひとつです。その特徴は、体が透明であること、20℃においてたった3日半で卵から大人になるライフサイクルの短さ、分子遺伝学的手法の簡便さなど、その研究のしやすさを挙げると枚挙にいとまがありません。それゆえ、線虫C. エレガンスはときに「究極のモデル生物」とも称されます。

線虫C. エレガンスのご活躍は、アンドリューブラウン著『はじめに線虫ありき』などに記されているので、詳細はそちらに譲るとして、本研究で最も重要視したその特徴は「小さいこと（約0.5mm）」と「大量に得られること」です。前述の研究のためには、実験室スケールで動物を大量に準備する必要がありますので、線虫は大きなポテンシャルを秘めた「アクティブマター」でした。

一方で、ひとつ大きな問題がありました。線虫は通常、寒天培地上に塗布した大腸菌を餌として培養するのですが、大腸菌を食べ尽くすと増殖は止まってします。増殖させ続けるために大腸菌懸濁液を供給し続けると、たちまち寒天培地上は水浸し（正確には大腸菌浸し）になってしまいますので、培養できる線虫の最大個体数には限界があります。そこで、我々は過去のある論文に目をつけました。

その論文では、C. エレガンスと異なる線虫種を「ドッグフード」で飼育していました。ドッグフードは犬が食べるだけあってとても栄養に富んだ食べ物です。既報に倣い、粉砕したドッグフードと混ぜた寒天で飼育したところ、大量のC. エレガンスを得ることに成功しました。

そして驚くべきことに、C. エレガンスは高密度のときに、群れてネットワーク状の秩序構造を形成することを発見しました。ここに、ついに実験室スケールの動物の群れを実現するに至ったのです。では、なぜ自分の位置を把握していない線虫が、動き回るだけで自発的に秩序構造を創出できるのでしょうか？

実験とシミュレーションによる群れ形成メカニズムの解析

私たちはまず、線虫1個体レベルの観察を行い、その結果をもとにビチェックらのモデルを改変しました。オリジナルのビチェックモデルでは、(1) 局所的に近接する自走粒子同士が方向を揃える配向相互作用が重要な物理的ルールです。私たちはこれに、(2) 個々の線虫が弧を描く動きをすることを2つ目の物理的ルールとして追加しました。

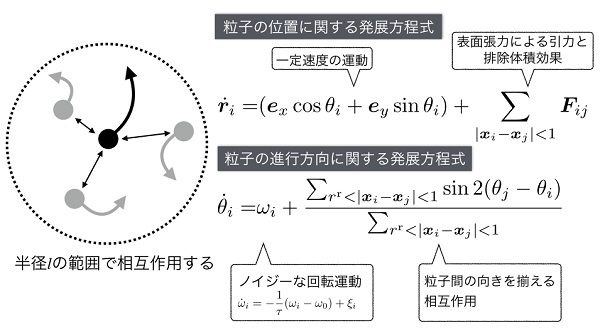
この数理モデルのシミュレーションの結果、線虫のネットワーク状の秩序構造がコンピュータ上で再現されました。続いて、さまざまな状況の実験結果を、対応するパラメータ下でのシミューレーション結果と比較することで数理モデルを検証しました。

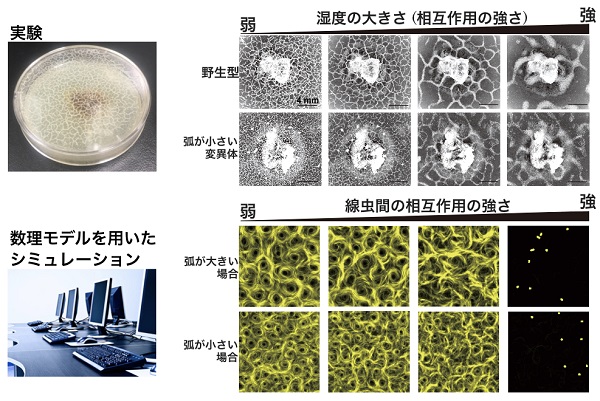
ここからが、C. エレガンスを用いた研究の真骨頂です。実験系は全体でも10cmに満たないので、周りの環境を容易に変化させることができ、線虫周囲の湿度や線虫密度といった条件を操作した実験ができます。

湿度を変化させたときのC. エレガンスの群れの様子

また、C. エレガンスには分子遺伝学的手法で同定された変異体が豊富に存在するため、たとえば描く弧の大きさが小さい線虫変異体を用いた実験を行うことができます。これらのように、さまざまな条件下での観察が可能なわけです。

得られた実験結果はシミュレーションと良く一致しており、(1)と(2)の物理的ルールが線虫の群れ形成の根幹をなすメカニズムであると私たちは結論づけました。

究極のアクティブマター「線虫C. エレガンス」？

現在、世界中でロボット開発が盛んに進められており、そのひとつとして単体では困難な作業を集団で行わせる群知能と呼ばれるアルゴリズムの開発が進められています。線虫は体長1mm弱のいわばマイクロマシンです。

したがって、今後、数理モデルによる予測精度を向上させ、線虫集団による秩序構造形成を自在に制御することができれば、そのアルゴリズムはロボット開発にも応用できるのではないかと思います。

今回私たちは、光刺激により制御する入力系を線虫ネットワークに与えることにも成功しています。光刺激を使えば多様な行動様式を実現できるので、集団運動に関する情報を増やして数理モデルの予測精度を向上させることができるでしょう。

遠い将来、このような基礎研究から応用研究へつなげることができれば、もしかすると線虫C. エレガンスが、「究極のアクティブマター」と称される日が来る、かもしれません…。

参考文献

Vicsek T, Czirok A, Ben-Jacob E, Cohen I, Shochet O “Novel type of phase transition in a system of self-driven particles” Physical Review Letters, 75, 1226 (1995)

アンドリューブラウン（著）、長野敬・野村尚子（翻訳）『はじめに線虫ありき』（青土社、2006年）

Tanaka R, Okumura E, Yoshiga T “A simple method to collect phoretically active dauer larvae of Caenorhabditis japonica” Nematology Research, 40, 7-12 (2010)

Sugi T, Ito H, Nishimura M, Nagai KH “C. elegans collectively forms dynamical networks” Nature Communications, 10, 683 (2019)