機械学習の関数「ボルツマンマシン」を用いて、量子多体系という難問に挑む
「量子多体系」とは?
量子力学の性質に従う多数の小さな粒子が相互作用しあう系を「量子多体系」と呼びます。たとえば、金属を冷やしていったときに電気抵抗が0になる超伝導現象や、磁石の性質を生み出す磁性の現象は、量子力学の法則に従う多数の電子が、互いに相互作用しあうことによって発現します。このように、量子多体系の理解は、身の周りの物理現象の解明には不可欠であり、新たな機能デバイスの開発にも欠かせない、非常に重要な課題です。
この記事では、機械学習の分野で学習機械として使われている「ボルツマンマシン」という機械が、量子多体系の性質を調べるうえでも有用であることを発見した研究について紹介したいと思います。
量子多体系の難しさと多体波動関数
量子多体系の性質は、量子力学において粒子が従うシュレーディンガー方程式(あるいはディラック方程式)の解である「多体波動関数」によって決定されます。したがって、多体波動関数がわかってしまえば粒子の運動が明らかになります。
しかしながら、系の自由度の数(粒子の数)が増えていくにつれて、波動関数の次元がものすごい勢いで(指数関数的に)増大するため、一般には解析的に厳密な多体波動関数を得ることができません。
たとえば、物質中に存在する電子の運動を量子力学の法則に則ってシミュレーションしようとすると、厳密な多体波動関数を用いたシミュレーションが可能なのは、せいぜい電子の数が数十個程度までに限られます。現実には、物質中にはアボガドロ数(6.02×1023)のオーダーの電子が存在するので、いかに量子多体系のシミュレーションが難しいかが、何となく実感できるかと思います。
それでは、完全にお手上げか? というと、そういうわけではありません。真の意味での厳密な波動関数は得られなくとも、近年急激に進歩を遂げている大規模数値計算によって、多体波動関数を精度よく近似するさまざまな手法が提案されてきています。そのため、年を経るごとに量子多体系の理解が徐々に進んできています。しかしながら、量子多体系のさらなる理解のためにも、より強力な数値計算手法の開発は大きな課題のひとつとなっています。
そこで著者らは、機械学習で用いられる関数が非常に高い関数表現能力を持っていることに着目し、多体波動関数を表現するのにも有用ではないかと考え、新たな手法の開発に至りました。
ボルツマンマシンとは?
本題に入る前に、本研究で使用した人工ニューラル・ネットワークの一種である「ボルツマンマシン」について簡単に紹介します。
私たちは、ボルツマンマシンのなかでも「深層ボルツマンマシン(DBM: deep Boltzmann machine)」という関数表現能力の高いボルツマンマシンを用いました。ボルツマンマシンは、可視層と隠れ層から成り立っています。ボルツマンマシンは確率分布を近似する機械であり、可視層のそれぞれの状態配置に対して確率を与えます。ここで、多体波動関数を(複素数に一般化した)確率を与える関数だと解釈すると、多体波動関数をボルツマンマシンによって書き表すことができます。
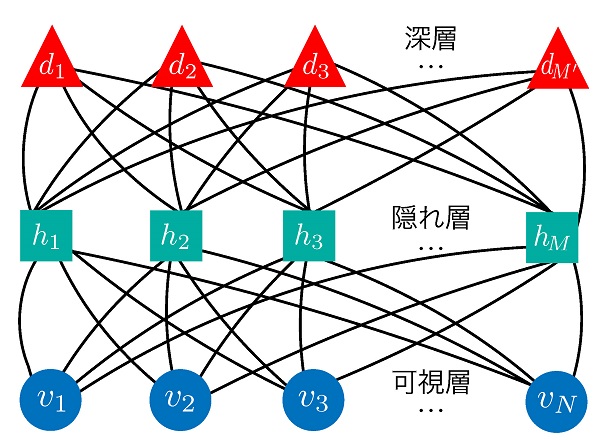
深層ボルツマンマシンは可視ユニット(丸)、隠れユニット(四角)、深層ユニット(三角)によって構成され、可視ユニットの状態を入力として、それぞれの状態に対して確率を与える機械である。ここで、2層ある隠れ層を区別するため、浅い隠れ層を単に隠れ層、深い隠れ層を深層と呼んで区別している。物理的自由度と可視ユニット自由度を同一視し、多体波動関数の値が、可視ユニットの状態配置に対する(複素数に一般化された)確率であると考えることで、多体波動関数をボルツマンマシンによって書き下すことができる。多体波動関数の形は、可視ユニット・隠れユニット間、隠れユニット・深層ユニット間の相互作用(実線)のパラメータの値に依存する。
ボルツマンマシンによって多体波動関数を表す
いよいよ本題です。本研究では、多体波動関数のなかでも、量子多体系において絶対零度で最も安定な量子状態である「基底状態」の波動関数を、深層ボルツマンマシンによって表現することを目指しました。
基底状態は次の方法で求めることができます。基底状態の成分を含む任意の量子状態に、ハミルトニアン1による微小な虚時間発展2を作用させると、その状態のなかから基底状態以外の成分が少し減ることがわかっています。そこで、基底状態の成分を含む任意の状態から微小虚時間発展を繰り返して状態を更新していくと、直観的には濁った水が多段階でろ過されていくプロセスに似て、最終的に基底状態だけが重みを持つようになり、基底状態が得られます。
つまり、量子状態を有限個のパラメータを持つ何らかの関数形で表現し、そこから虚時間発展を再現するようにパラメータを最適化していく(微小虚時間発展の度にパラメータが更新される)と、基底状態を表すことが可能になります。
しかしながら、既存の関数形は関数表現能力に制限があるために、この虚時間発展を厳密に追うことができず、基底状態を近似的にしか表現できませんでした。
それに対して、深層ボルツマンマシンを用いて量子状態を表現すると、その非常に高い関数表現能力のおかげで、虚時間発展を厳密に再現することが可能であることが示されました。
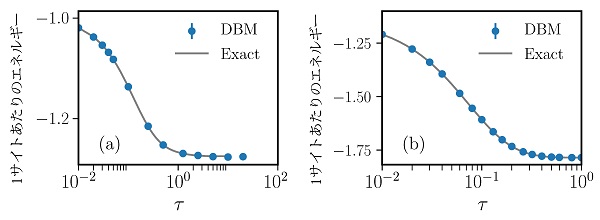
量子スピンが互いに相互作用しあう多体系の量子状態を深層ボルツマンマシン(DBM: deep Boltzmann machine)を用いて表現した。典型的な量子力学的スピン模型である(a) 1次元横磁場イジング模型、(b) 1次元反強磁性ハイゼンベルグ模型に対するDBM量子状態のエネルギーの虚時間発展のベンチマーク。手法が正しいかを確かめるため、サイズの小さい系(それぞれ20サイト、16サイト)に対して適用し、厳密対角化によって得られた厳密な虚時間発展(実線)と比較している。実際には、厳密対角化が適用不可能な大きな系(40~50サイト以上)に対しても、深層ボルツマンマシンの手法は適用可能である。
このことにより、深層ボルツマンマシンによって基底状態を任意の精度で表現することが可能になりました。
言い換えれば、虚時間発展というツールを用いて深層ボルツマンマシンが多体波動関数を学習したといえます。系のエネルギーなどの物理的な性質は、得られた深層ボルツマンマシン状態をもとに数値計算によって求めることができます。
おわりに
本研究によって、高い関数表現能力を持つ機械学習の関数が、量子多体波動関数の表現にも有益であることが示されました。機械学習と物理という異なった分野間の交流により、今後ますます強力な数値手法の開発につながっていくと期待されます。そのため、機械学習による量子多体波動関数の表現は、量子多体系に対する我々の理解の促進にはずみをつける成果といえます。
参考文献
Giuseppe Carleo, Yusuke Nomura, and Masatoshi Imada, “Constructing exact representations of quantum many-body systems with deep neural networks” Nat. Commun. 9, 5322 (2018)
脚注
1. ハミルトニアン:系のエネルギーを表す演算子。ハミルトニアンを行列表示すると、その行列のサイズは系の自由度の数に対して指数関数的に大きくなる。この莫大なサイズの行列の固有ベクトルが系の固有状態に対応し、そのなかでも一番エネルギーの低い状態を基底状態という。
2. 虚時間発展:ハミルトニアンによる実時間発展は、実数の時間tに対してどのように系が時間発展するかを表しているが、虚時間発展はそれに対して虚軸方向の”時間”itへ系がどのように変化するかを表す。実時間発展が系のダイナミクスに対応するのに対し、虚時間発展は系の温度の上下に対応する。虚軸の正の方向に虚時間発展すると有効的に系の温度が低下していく。したがって、基底状態を含む量子状態から虚時間発展すると、系の温度の低下に伴い、最終的に絶対0度で一番安定な基底状態のみの成分だけ取り出すことができる。
この記事を書いた人

-
野村 悠祐(のむら ゆうすけ)
理化学研究所 創発物性科学研究センター 研究員(2019年4月より)。
2015年3月に東京大学大学院博士課程修了。2015年4月から2016年8月までエコール・ポリテクニークでポスドクをしたのち2016年9月から東京大学大学院 工学系研究科 物理工学専攻 助教。2019年4月より現職。
専門は物性理論、計算物質科学。強相関電子系を第一原理的に研究する数値計算手法の開発・応用に興味を持っている。近年は機械学習の技術を物性分野に応用ができないか模索している。