ミツバチがつくる「ハニカム構造」の謎 – ミツロウの自己組織化をシミュレーションで検証する
ハニカム構造の謎
人類はミツバチと長い歴史を共にしてきました。採蜜は一万年前から行われているとされ、ハチミツやロイヤルゼリーは貴重な栄養源として重宝されています。また、ミツバチの巣に見られる精緻な「ハニカム構造」は、古くから科学的関心を集めてきました。

ミツバチの巣は、働きバチが分泌するミツロウからできています。ハニカム構造は耐久性と貯蔵性に優れており、作製に必要な材料を少なくできる利点があるため、ミツバチは進化の過程でハニカム構造を作る能力を獲得したと考えられています。
しかし、どのようにしてミツバチがそのような精緻な構造を作るのか、そのメカニズムは謎に包まれています。営巣メカニズムの解明は、社会性昆虫の代表例であるミツバチの生態を理解するうえで重要なものであり、さらにバイオミメティクスによる応用にも寄与する可能性を秘めています。
そこで私たちは、実際にミツバチを飼って営巣の様子を観察しながら、ミツバチがハニカム構造を作るメカニズムの本質を理解するために研究を進めています。
ミツバチは器用な建築家?
ミツバチが精緻なハニカム構造を作る謎について、大きく分類すると2つの有力な説があります。ひとつは、ミツバチが発する熱でミツロウが溶けて、表面張力によりハニカム構造が現れるという説です。もうひとつは、ミツバチ自身が「器用な建築家」としてハニカム構造を作製するという説です。ただし、前者の説に関しては、これまでのところ営巣の際にミツロウが溶けている様子が直接観察されたという報告はありません。
こうした状況を踏まえて、私たちはミツバチを「器用な建築家」とみなして研究を行いました。ただ、いくらミツバチが器用な建築であったとしても、小さな脳しか持たず、働きバチの寿命が長くて半年程度しかないことを考えると、働きバチが人間のように系統立ててハニカム構造を作製しているという描像は非現実的です。
そこで私たちは、ミツバチが本能として世代間で受け継ぐことのできる単純な行動により、ボトムアップ的にハニカム構造を作製していると考えました。
ミツロウの付着と掘削による自己組織化
ボトムアップ的な構造物作製のひとつの手段として、「自己組織化」が挙げられます。自己組織化とは、構成物間の局所的な相互作用により、大域的な秩序化が自発的に起こる過程のことをいいます。
自己組織化の代表例として、レイリー・ベナール型対流の形成が挙げられます。レイリー・ベナール型対流の形成では、系へのエネルギーの供給と排出がうまくつりあうことが肝心です。この例のように、自己組織化が起こるためには何らかの供給と排出が起こる必要があり、ミツバチの巣作りではミツロウがそれにあたると私たちは仮定しました。
ミツロウの供給は、働きバチがミツロウを付着することでなされます。一方、ミツロウの排出は、働きバチがミツロウを掘削することでなされると考えました。働きバチがミツロウを掘削することはこれまでにも知られていましたが、営巣過程への掘削の影響は明らかではありませんでした。
そこで、ミツロウを掘り進められるところまで掘り、ミツロウが一定の厚みより薄くなると掘削をやめるという条件を設定することで、営巣過程で掘削が果たす役割を具体的に仮定しました。
こうして、働きバチによるミツロウの付着と掘削という行動ルールに従って、自律的に行動する対象(エージェント)と、それらのあいだの相互作用を設定した現象論的なモデルである「付着・掘削モデル(attachment-excavation model)」を提案し、コンピュータシミュレーションによって平面上でどのような構造が得られるのかを調べました。
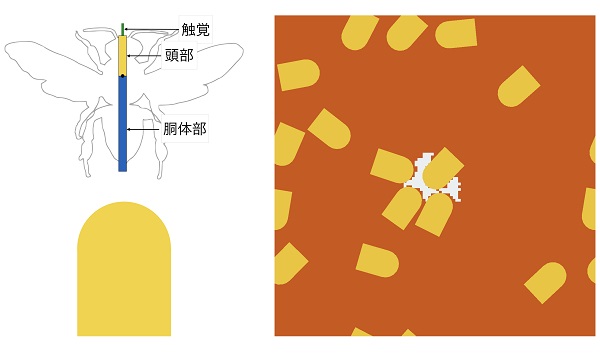
(左上)働きバチを触覚、頭部、胴体部により抽象化したもの
(左下)エージェントの形状。形状は抽象化された働きバチが掘削できる領域に対応しており、ミツバチが前後に動きながら周囲を掘削することから長方形と半円が接合した形状としている。
(右)コンピュータシミュレーションのスナップショット。平面上(茶色)を運動する多数のエージェント(黄色)により、時々刻々と変化するミツロウ(白色)のパターンが得られる。
単純な行動ルールによって作られる精緻な構造
ミツバチの営巣過程では、まず三角錐の面が凹んだような形状の構造物が作られ、この構造物を最小構成単位として一方向に連結したものがハチの巣の土台となります。
「付着・掘削モデル」のコンピュータシミュレーションでは、この初期構造を再現することができ、さらに、ミツロウが一方向に付着しやすいという追加設定のもとでは、ハチの巣の土台となる構造も再現されました。
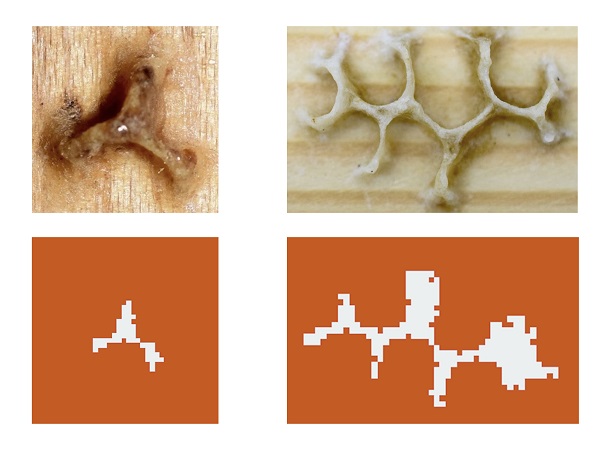
(左下)コンピュータシミュレーションにより得られた、営巣初期過程で見られる構造に対応したパターン。白色部分がミツロウを表す。
(右上)ハチの巣の土台となるミツロウの構造で、最小構成単位が一方向に連結したものとみなせる。
(右下)コンピュータシミュレーションにより得られた、ハチの巣の土台となる構造に対応したパターン。
これらの結果は、「付着・掘削モデル」の正当性を支持するもので、ミツロウの付着と掘削という単純な行動ルールに基づいた活動によって、精緻な巣が作られうることを明らかにしました。
営巣メカニズムの解明とその応用の可能性
私たちは、ミツバチの行動ルールに基づいて「付着・掘削モデル」というエージェントベースモデルを提案し、そのコンピュータシミュレーションを実行しました。その結果、ミツロウの付着と掘削という互いに相反する行動ルールの競合による自己組織化で、複雑な構造が創発するという描像により、営巣初期過程が説明できました。これは、ミツバチが「自己組織化をうまく活用する建築家」であることを示唆するものとなっています。
「付着・掘削モデル」は営巣の全過程を説明することを意図して作られたモデルのため、今後は3次元シミュレーションによって巣の立体構造を再現することを目指します。その過程で、「付着・掘削モデル」に対する検証・改善を繰り返すことで、営巣メカニズムの本質に迫ります。また、「付着・掘削モデル」を粗視化して得られる数理モデルの作成も準備しており、営巣メカニズムの解明に向けた研究を多角的に進めます。
さらに応用面では、ミツバチの行動ルールが明らかになることで、構造物作製における可能性が広がります。たとえば、ナノスケールで動く機械を考えたとき、その機械に複雑な行動ルールを課すことは難しいでしょう。しかし、ミツバチに倣うような単純な行動ルールを設定したナノマシンが用意できれば、ナノサイズのハニカム構造を作製するといったことも可能となるかもしれません。
参考文献
- Narumi T, Uemichi K, Honda H, Osaki K “Self-organization at the first stage of honeycomb construction: Analysis of an attachment-excavation model” PLoS ONE 13(10): e0205353 (2018) https://doi.org/10.1371/journal.pone.0205353
- 鳴海 孝之『ミツバチの造巣初期過程に対するエージェントベースモデル』(数理解析研究所講究録 2043: 142. 2017)
この記事を書いた人

-
鳴海 孝之(写真左上)
山口大学大学院創成科学研究科講師。2005年慶應義塾大学理工学部物理学科卒業、2010年東北大学大学院工学研究科ナノメカニクス専攻博士課程修了。博士(工学)。九州大学、関西学院大学、九州産業大学を経て、2017年より現職。研究分野は統計物理学で、複数の効果が競合することで創発する動的パターンに興味を持ち、物性理論および計算機シミュレーションによる研究を進めている。日本物理学会、形の科学会会員。その他の研究についてはWebサイトを参照のこと。
上道 賢太(写真右上)
関西学院大学大学院理工学研究科博士課程後期課程在籍。2012年同大学物理学科数学専攻卒業、2014年同大学院博士課程前期課程数理科学専攻修了、修士(理学)。学部時代より反応拡散方程式系に見られる時空間パターンの形成について研究を行っている。自然界が作り出す美しい幾何学パターンのひとつとしてハニカム構造に興味を持ち、営巣のメカニズムを解明することを目指している。現在は、中学校数学教員として勤務しながら研究を続けている。
本多 久夫(写真左下)
神戸大学大学院医学研究科客員教授。1965年京都大学理学部物理学科卒業。同大学大学院修士課程・博士課程を経て鐘紡株式会社鐘紡ガン研究所(1975-1996年)、兵庫大学(1996-2013年)を経て現在に至る。専門は理論生物学。形の科学会、日本発生生物学会会員。著書に『形の生物学』(NHKブックス、2010)など。
大﨑 浩一(写真右下)
関西学院大学理工学部教授、関西学院大学数理・データ科学教育研究センター長。1995年神戸大学理学部数学科卒業、2001年大阪大学大学院工学研究科応用物理学専攻博士後期課程修了、博士(工学)。2013年より現職。化学走性に起因する生物移流等を伴う反応拡散系に対する解の存在とその挙動の研究に従事。また、大学所有のキャンプ場にて養蜂をしながら、営巣のメカニズムも研究している。日本数学会、日本数理生物学会、兵庫県生物学会、国際数理科学協会会員。




