スイマー・マイクロレオロジー:ソフトマター中のマイクロマシンの新しい遊泳機構
微生物の遊泳原理:「ホタテ貝の定理」
遊泳するマイクロマシン(スイマー)の研究は、バクテリアや精子などの微生物の流体内運動との関連で注目を集めています。一般的にスイマーは、自身が持つ可動部位を周期的に形状変形させることで前進します。水のような粘性流体中のスイマーの運動に関しては、Purcellによって提唱された「ホタテ貝の定理」と呼ばれる力学的な制約があることが知られています。この定理によると、慣性が無視できる微小な物体は、その形状変形の時間反転対称性が保たれている(すなわち往復的な形状変形である)限り、変形によって移動をしても一周期後には再び元の位置に戻ってしまいます。たとえば、水中のホタテ貝が2枚の貝を開閉させるだけでは、同じ場所を中心に前後に振動するだけで、遠くへ移動できません。
そのため、粘性流体中でスイマーが移動するためには、何らかの時間反転対称性を破る形状変形が必要となります。いくつか提唱されている遊泳モデルの中で、NajafiとGolestanianによって考案された「三つ玉スイマー」は、粘性流体中で並進運動を獲得するミニマムモデルになっています。三つ玉スイマーは2つの可動アームを持っており、アーム運動の時間反転対称性を破ることによって一方向に遊泳することができます。
細胞の粘弾性を測定:マイクロレオロジー
一方、マイクロレオロジーとは、コロイド粒子などの微粒子のブラウン運動や外力に対する応答を検出することによって、高分子溶液やゲルなどのねばねばとしたソフトマターの粘弾性を調べる最先端の実験手法です。ここでレオロジーとは、物質の変形や流動を扱う学問であり、粘弾性とは、物質が変形の周波数に応じて粘性的(液体的)や弾性的(固体的)に振る舞う性質を意味しています。
最近では、マイクロレオロジーの手法を使って、生きている細胞1個の力学応答や粘弾性的な性質も測定できるようになっています。また微粒子のブラウン運動を観察するパッシブ・マイクロレオロジーと、光ピンセット法(集光したレーザー光を用いて微小物体を操る方法)で微粒子に外力を加えるアクティブ・マイクロレオロジーを組み合わせることで、細胞や生体系の非平衡性を定量的に調べることが可能になりつつあります。
ソフトマター中のスイマー:「ホタテ貝の定理」の破れ
我々の研究グループは、水のようなさらさらとした粘性流体中ではなく、ソフトマターのようなねばねばとした粘弾性体中を遊泳するマイクロマシンの動作機構について理論的に考察しました。具体的には、アクティブ・マイクロレオロジーで使われている基本式を三つ玉スイマーに適用することで、スイマーの遊泳速度とソフトマターの複素粘性率を結びつける関係式を導出しました。この複素粘性率は周波数に依存しており、その実部と虚部がそれぞれ粘弾性体の粘性率と弾性率の情報を含んでいます。
この関係式によると、スイマーが粘弾性体中を遊泳する場合、必ずしも「ホタテ貝の定理」が成り立たないことがわかりました。すなわち、粘弾性体中のスイマーは、たとえその形状変形の時間反転対称性が保たれていても、スイマー自身の構造対称性が破れていれば、有限の速度で移動可能であることが理論的に示されました。三つ玉スイマーの場合、2つの可動アームの振幅を異なる長さに設定することによって、スイマーの構造対称性を破ることができます。
新しい測定手法:スイマー・マイクロレオロジー
得られた遊泳速度について、媒質が水のような粘性流体である極限を考えると、Golestanianらによって得られた以前の関係式に帰着します。また、スイマーの構造対称性を保持すると、粘弾性体の粘性率のみの情報が得られます。そのため、このたび三つ玉スイマーで得られた表式は、ソフトマター中のスイマーの運動に関する「一般化されたホタテ貝の定理」を示唆する結果になっています。すなわち、三つ玉スイマーがソフトマター中を遊泳するには2通りの可能性があり、一方は形状変形の時間反転対称性を破ることであり、他方はスイマーの構造対称性を破ることです。前者の機構はソフトマターの複素粘性率の実部(粘性率)を、後者の機構はその虚部(弾性率)をそれぞれ反映するため、両方の機構を独立に測定することにより、媒質としてのソフトマターの粘弾性的性質が明らかになります。
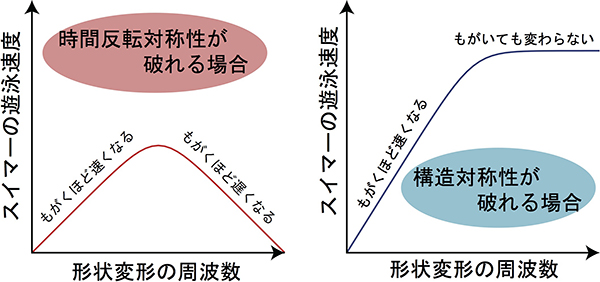
このように、スイマーの平均遊泳速度からソフトマターのレオロジー的性質がわかるため、本論文で提唱された測定手法は「スイマー・マイクロレオロジー」と命名されました。この研究成果は、ソフトマター中のマイクロマシンの遊泳機構を与えるとともに、新しいタイプのアクティブ・マイクロレオロジーの基本原理となることが期待されます。
本研究は、これまでほぼ独立に行われてきたマイクロスイマーの研究とマイクロレオロジーの研究を融合するものになっています。具体的な予測のひとつとして、特徴的な緩和時間をもつ典型的なソフトマター中では、スイマーの形状変形の周波数を大きくすればするほど(もがけばもがくほど)遊泳速度は却って遅くなる場合があり、これは我々の日常感覚とも一致します。今後は三つ玉スイマー以外のより一般的なモデルでの理論的な取り扱いや、構造非対称性を有するマイクロスイマーを実際に構築することが望まれます。
将来の夢:非平衡系のマイクロマシン
一般に微生物が遊泳する環境は単なる粘性流体ではなく、ソフトマターのように粘弾性的な振る舞いを示す場合が多いことが知られています。今回三つ玉スイマーの遊泳で得られた知見は、ソフトマター中のバクテリアの運動や、細胞の鞭毛運動、繊毛の波打ち運動などを理解するための重要な指針となるでしょう。逆に微生物の運動様式を調べることによって、微生物が住む環境の粘弾性の情報を得ることも可能となります。
微生物よりもさらに小さなスケールに注目すると、たとえば細胞内のように多数の生体分子で混み合った環境も粘弾性的性質を示し、細胞中の物質輸送に大きな影響を及ぼします。近年では、細胞内における非平衡性と粘弾性に起因する異常な拡散現象が実験的に報告されており、細胞内のゆらぎや物質移動の違いから正常細胞とがん細胞を識別する新しい医療診断法にも期待が高まっています。スイマー・マイクロレオロジーの概念は、粘弾性的な細胞内の様々な動的現象や非平衡現象の理解の一助となると考えられます。
一方、分子マシンは2016年のノーベル化学賞の受賞対象となりましたが、真に機能するマシンを構築するためには、環境の粘弾性を考慮することが重要であり、さらに分子構造として導入すべき非対称性を精密に設計する必要があることが、本研究より明らかになりました。新たに提唱されたスイマー・マイクロレオロジーのアイディアをきっかけとして、将来的にはマイクロマシンやナノマシンの実現に向けた基礎と応用の両面にまたがる新しい研究の展開が期待されます。
参考文献
E. M. Purcell, Am. J. Phys. 45, 3 (1977).
A. Najafi and R. Golestanian, Phys. Rev. E 69, 062901 (2004).
K. Yasuda, R. Okamoto, and S. Komura, J. Phys. Soc. Jpn. 86, 043801 (2017).
この記事を書いた人

-
安田健人(写真左)
首都大学東京・理工学研究科・博士前期課程。2016年首都大学東京都市教養学部卒業。細胞中の非平衡現象に注目し、理論的な手法で研究している。これまでに細胞膜の非平衡ゆらぎや非平衡環境下における異常拡散について研究してきた。最近はマイクロマシンが細胞中の輸送現象の理解に役立つと考え、興味を持っている。
岡本隆一(写真中央)
首都大学東京・理工学研究科・特任助教。博士(理学)。2007年慶應義塾大学理工学研究科後期博士課程修了。京都大学理学部博士研究員、同大学福井謙一記念研究センターフェローを経て、2014年より現職。
好村滋行(写真右)
首都大学東京・理工学研究科・准教授。理学博士。1991年東京大学理学研究科博士課程中退。東京工業大学理学部、京都大学理学部、九州工業大学情報工学部、ヴァイツマン科学研究所、東京都立大学理学研究科を経て、2005年より現職。




