構成概念の測定：未完のプロジェクト

社会学や心理学、経済学、政治学、教育学など社会科学の分野では、測定が困難な構成概念（construct）を扱うことが多いです。たとえば、巷で「能力」と呼ばれているものは、何となくのイメージは浮かびますが、いざ測定するとなるとどのように測定すれば良いのか、何かしらの枠組みにしたがって「構成概念」に操作的定義を行ったうえで、あくまで観測可能な代理指標（proxy variable）を用いて間接的に実証分析を行うことが基本です。

一般的に、調査設計の工夫によって、正確な測定を心掛けながら、構成概念と代理指標の隔たりをできるだけ小さくすることが鉄則です。しかしながら、測定したいものが「構成概念」である以上、どれだけ頑張って調査設計の工夫をしても、「完璧」な測定はあり得ないことでしょう。ゆえに、測定したものに対して、これが理論上の「能力」を適切に反映しているのか、という代理指標の妥当性に関する議論が必ず生じます。

ただし、測定指標の精度を高めれば、それを用いたときの実証分析も必ず精緻になるのでしょうか。直感的にはそのように思われがちですが、実際のところ、構成概念と代理指標の隔たりを小さくする調査設計の工夫がどれだけ報われているのか、わからない部分もあります。つまり、構成概念を正確に測定できなかったとしても、実証分析の結果へ大きな影響を与えないというケースは考えられないでしょうか。そこで私たちは視点を変え、構成概念と代理指標の不一致を受け入れたうえで、感度分析（Sensitivity Analysis）から、分析結果がどの程度、信頼に足るものなのか、どのようなバイアスを伴っているかということについて事後的に検討するための手立てを考えるために、バイアスの定量化を試みました。

交絡変数と統計的因果推論への着目：部分的統制と合流点バイアスのジレンマ

バイアスの定量化といっても非常に広いので、私たちは、ひとまず統計的因果推論を行うときに、交絡変数で代理指標を使用することの是非に着目しました。交絡変数を考慮した最も簡単なモデルは次のようなDAGで表現できます。

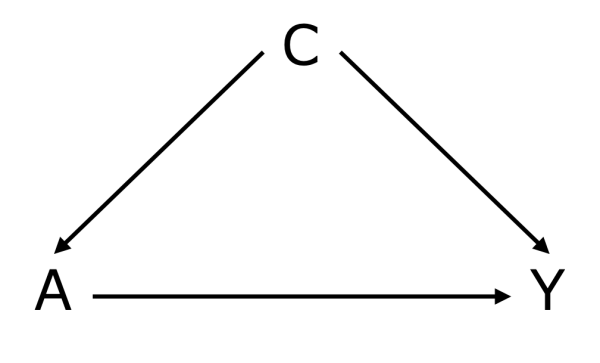
たとえば、SES（Social Economics States）は、まさに社会科学研究ではよく交絡変数とされるもののひとつです。たとえば、学歴と自尊感情との因果効果を調べる場合、SESはまさに重要な交絡変数とされます。SESは学歴と自尊感情の双方に同時に正の影響を与えるので、式1.のように統制せずにA→Yの因果効果を推定すると、推定値b1**にはSESによる影響も混入し、過大評価になりかねます。このときの推定バイアス（推定値と真値との差分）をa-biasとします。

式2.のように、交絡変数（C）であるSESをもし統制出来たら、回帰係数b1はA→Yの真の因果効果の不偏推定量となります。一方、すでに論じたように、SESは構成概念であり、実証分析ではアンケートを通して「家庭収入」などの代理指標を尋ねることになります。この場合、統制できるのは代理指標（P）であり、式3.が示しているように、因果効果の推定値がb1*になります。代理指標Pは、真のCの情報の一部のみ持っているので、SESによる影響の混入はある程度抑制できるものの、一定の推定バイアスがなお残されます。それをp-biasとします。


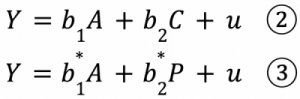
感覚的には、部分的統制（partial control）に過ぎないとはいえ、代理指標を統制したほうが良いだろうと思われますが、実は、代理指標（P）の生成過程に、従属変数（Y）の誤差項が関連してしまう場合、必ずしもそうとはいえません。たとえば、アンケートで得られた「家庭収入」はいわゆる社会的望ましさバイアスにより、回答者が「見栄っ張り」であるほど、水増しして記入することも考えられます。この状況をDAGで次のように表現できます。

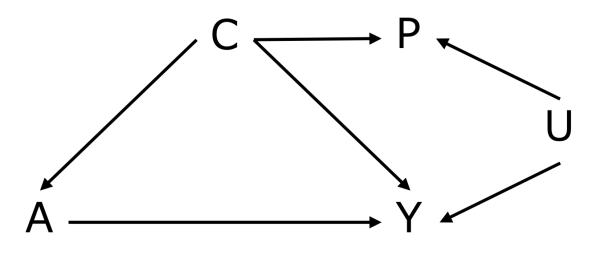
実はこの場合、統制変数の選定に関するジレンマが起きてしまいます。ある変数を統制するかについての判断は一般的には「バックドア基準」に従います。バックドア基準の詳細については割愛いたしますが、結論から言うと、A←C→P←U→YというバックドアパスがPの統制によって開いてしまい、いわゆる合流点バイアスが生じるということになります。

ゆえに、代理指標Pには一部交絡変数Cの情報が入っているので、A←C→Yというバックドアパスを部分的に統制できますが、同時にA←C→P←U→Yというバックドアパスが新たに生じてしまい、合流点バイアスを導入することになります。

このように交絡変数の代理指標を統制すべきものか否かに関するジレンマに陥ります。

ジレンマのなかで統制の是非を判断：p-biasの挙動について

内生性問題の部分的統制と合流点バイアスのジレンマ状態になっている以上、代理指標の統制についてさらに精緻な議論が必要であることが言うまでもありません。具体的に言うと、そういう代理指標を統制した場合の推定バイアスp-biasと統制しない場合の推定バイアスを定式化し、|a-bias|との大きさの関係について判断することになります。

結論から言いますと、p-biasの定式は四つのパラメータから表現できます（式4.）。即ち、1.交絡変数Cがどれだけの内生性問題を引き起こすかを示すパラメータq1（即ちa-bias）、2.代理指標Pがどれだけ交絡変数Cを反映しているかを示すq2（Cからの影響をUからの影響で割ったもの）、3. Aの誤差分散A（Cによって説明されない部分の分散）、そして4. Yの誤差分散Y（Uの分散）です。

 

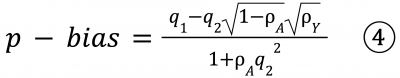
四つのパラメータのうち、代理指標の性質とかかわっているのはq2のみです。q2が大きければ大きいほど、代理指標は測定誤差が抑えられ、交絡変数Cの真値をより反映できた精度の良いものといえます。では、統制するべきか否かの判断がいかに代理指標の性質によって変わるだろうかを明らかにするために、本研究は、q2によるp-biasの挙動を確認しました。詳細な数理モデルとシミュレーションのセットアップは、論文を参照してもらうこととして、以下では、p-biasの挙動の図示と結論を簡潔に紹介します。なおモデルを簡単化するためにすべての変数の係数が正とします。

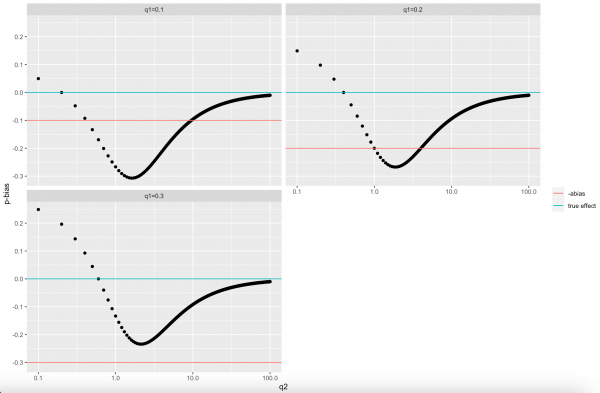
この図からわかるように、交絡変数Cを反映している度合い（=q2）が大きくなるにつれて、p-biasは次のように挙動します。

まず、q2=0のときに、代理指標Pには交絡変数Cの情報をまったく反映しておらず、内生性問題の部分的統制も合流点バイアスもそもそも生じていません。このときのp-biasは即ち何も統制しないときのa-bias（q1）です。q2（交絡変数Cの反映度合い）が大きくなるにつれて、p-biasが徐々に小さくなり、 のときにp-biasが偶然にも「0」となります。その後、p-biasが引き続き下降し、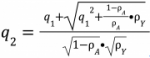 のときに下限値をとります。それから、「0」に漸近していきます。

上記の挙動から、p-biasの上限がa-biasであることが明白です。一方、p-biasの下限値はマイナスa-biasよりも低い場合が考えられます。つまり、q2がある区間に位置すると、合流点バイアスの影響が大きくなり、負の方向へと極めて激しいバイアスがもたらされるかもしれません。またこの区間において、常識に反していることも起きています。即ち、一般的に、測定誤差を抑えて代理指標の精度を高めると分析結果がより正確になると思われるが、実は、この区間において下限値をとるまでは、q2の増大（指標精度の向上）が逆に、負のバイアスを拡大させています。

また、a-biasとの比較でいえば、q1=0.1の場合、p-bias<|a-bias|の範囲が比較的大きいですが、q1=0.3の場合、常にp-bias<|a-bias|となります。つまり、q1が大きければ、合流点バイアスが生じたとしても、代理指標を用いた部分的統制によって真値に近い推定値が得られます。逆に、q1が小さければ、元々大きな脱落変数バイアスを引き起こしているわけではないため、わざわざ代理指標Pを統制して合流点バイアスを新たに導入するリスクを負う必要がないといえます。

とはいえ、指標の精度が無限に大きくなると、p-biasが0に近づいていくことも示されています。ゆえに、q2の増大が逆にバイアスの拡大につながる区間のあるものの、指標の精度をできるだけ高めようという方針には一理あるともいえます。ただし、この論文をさらに複数の交絡変数に対してひとつの代理指標というモデルに拡張して検討すると、p-biasの漸近値がそもそも0になる場合がごくまれであることがわかりました。（樊ほか2022）。つまり、交絡変数Cを反映している度合いが無限に大きくなったとしても、むしろ推定値がどんどん真値から離れていくことが示されています。

以上が大まかな結論ですが、この研究論文で検討した因果モデルは、あくまでも交絡変数がひとつしかない単純な因果モデルを想定していました。現在は、このような複雑なモデルへの拡張や、交絡変数以外に従属変数などにも焦点を当てており、欠損バイアスとのトレードオフ関係の検討など、研究を進めています。最後に、本研究はあくまでも極めて単純化された因果モデルでしたが、状況によっては、正確な測定がバイアスの小さな統計的因果推論に繋がらないことを例示しました。このことが、調査法や社会科学の統計分析における何らかの議論を誘発できれば、本研究に一定の成果があったのではないかと思っています。

 

参考文献

  • Elwert, Felix and Christopher Winship, 2014, “Endogenous Selection Bias: The Problem of Conditioning on a Collider Variable,” Annual Review of Sociology, 40(1): 31-53.
  • 中尾走・樊怡舟・村澤昌崇、2022、「交絡変数の測定誤差が合流点バイアスをもたらす影響について」『理論と方法』71：34-52.
  • 樊怡舟・中尾走・村澤昌崇、2022、「交絡変数の測定誤差が合流点バイアスをもたらす影響について（2）：複数の交絡変数への拡張」広島大学高等教育研究開発センター編『Advancement of Higher Education Research: RIHE Monograph Series』6：1-23.

この記事を書いた人

中尾走 樊怡舟
中尾走
愛媛大学工学部で学士（工学），愛媛大学大学院教育学研究科で修士（教育学）広島大学大学院教育学研究科博士課程後期・日本学術振興会特別研究員（DC2）で博士（教育学）を取得。進学する度に専門を変えながらふらふらとしたキャリアを経て，現在は，広島市立大学大学評価・IRセンター特任助教。ふらふらとしたキャリアを経ていない自分を観察してみたい。

樊怡舟
現在は，広島大学高等教育研究開発センター　研究員。中国上海出身で、2015年より広島大学大学院に留学し、以降高等教育を専攻し、2022年に博士学位を取得しました。研究関心は教養教育カリキュラム開発や研究資金配分など高等教育分野の研究課題のほかに、社会科学における数理モデルの可能性・限界など方法論的検討にも興味を覚えています。