原子層結晶で電子スピンが現われる仕組みとは？ – 超高分解能測定で探る

「原子層結晶」の特異な性質とは？

物質の厚さを原子レベルまで薄くすると、その性質はどのように変わるでしょうか？ たとえば、グラファイトを原子1層まで薄くしたグラフェンでは、電子が高速移動できるようになります。このように、原子レベルまで薄くした物質には新たな興味深い性質が生じることがあります。

固体表面上に作製した原子1層から数層の厚さを持つ「原子層結晶」は、薄くしたことによる性質に加え、層垂直方向の反転対称性が破れていること（層の片側が固体表面、反対側が真空もしくは大気となっていること）による新奇物性が発現する可能性を秘めた物質です。

反転対称性が守られている固体内部では、原子が3次元に規則的に配列しているため、原子核周りの電子の密度は一様となっています。これに対し、原子層結晶では層の上下で結合状態が異なって反転対称性が破れた状態となっていることから、原子核周りの電子の密度に片寄りができます。この電子の密度の片寄りは、原子層に垂直な方向に電池のように電位差（電場）を生じさせたり（電子の密度が一様だと電位差はできません）、原子核の上下で電子の非対称な運動を誘起します。

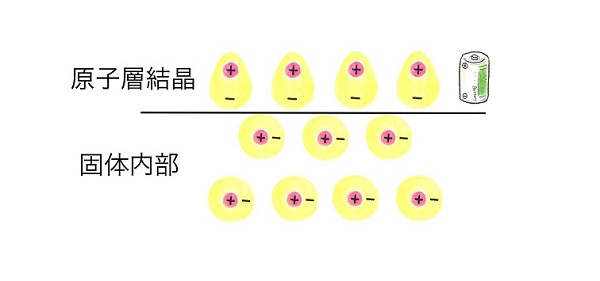
原子層結晶の電子バンドは分裂する

電子は自転運動しながら原子核の周りの軌道を運動しています。電子スピンは電子の自転運動に対応するもので、その向きは自転軸方向への回転の向きによって決まると考えることができます（電子スピンが整列した状態となっていると物質は磁石になることから、電子スピンを電子磁石と考えることもできます）。

この電子スピンと軌道は、相対論効果であるスピン軌道相互作用によって影響しあっていますが、反転対称性が守られている非磁性固体中ではその影響が無視でき、反対の方向を向く2つの電子スピンが対になって運動します。これは、固体中の電子の運動量と束縛エネルギーの関係を示す電子バンドを観測したとき、異なる2つの向きの電子スピンのバンドが縮退（重なっている）ことに対応しており、光電子分光による実験で確認することができます。スピンが縮退した電子バンドを有する試料では、電子の運動と平行方向に電場をかけるとスピンの情報が打ち消された電荷の情報だけが流れる「電流」となります。

これに対し、反転対称性が破れた「原子層結晶」では、スピン軌道相互作用の影響で電子バンドが反対方向を向く、2つのスピン偏極した電子バンドに分裂します。

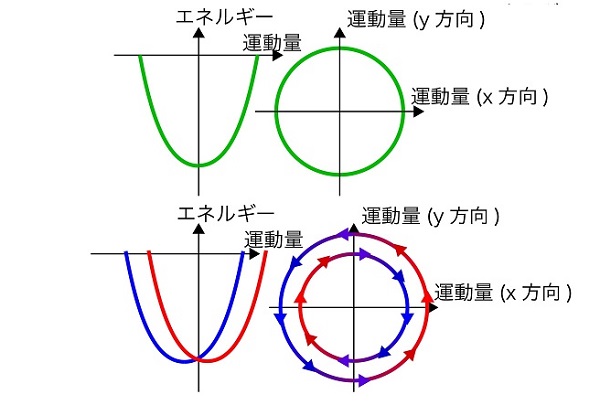
スピン偏極電子の起源とは？

このときのスピンの向きは「フレミングの左手の法則」で考えることができます。原子面に垂直な方向の電子の密度の片寄り（電池）を親指方向にとったとき、中指方向に電子が動くと磁場（磁石）は人差し指の方向を向きます。

電子磁石と考えることができる電子スピンは磁場と平行方向になるので、反転対称性の破れによる非対称な電子密度を考えた電子スピンの向きは、常に原子面に平行で電子の運動方向に垂直となります。これは「ラシュバ効果」と呼ばれており、これまで原子層結晶に生じるスピン偏極電子の起源であると信じられていました。

ここで、スピン偏極した電子の速度は、スピンの向きが磁場と平行のときは反平行のときよりも速いため、電子が運動する原子層に平行な方向の電場をかけたときに、電荷の情報に加えてスピンの情報が流れる「スピン流」が流れます。

これまで、理想的なラシュバスピンとは異なる特異なラシュバスピンの要因は、原子層結晶の構造の対称性など、その時々で異なる理由によってこれまで説明されていましたが、普遍的な理解は得られていませんでした。

超高分解能測定でみえた電子スピンの振る舞い

我々は、原子層結晶における電子スピンの動きの普遍的な理解を目指して、「超高分解能角度分解光電子分光」および「スピン分解角度分解光電子分光」によって、シリコン表面に作製したインジウム2層からなる原子層結晶の電子状態を測定しました。シリコン上のインジウムは、インジウム結晶と非常に近い格子定数の原子層結晶を作ります。

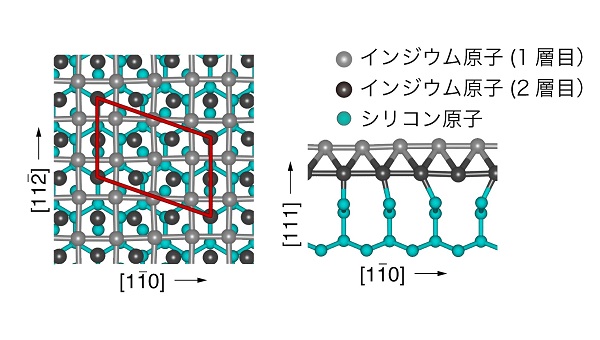
この原子層結晶のフェルミ準位での運動量面（フェルミ面）には、蝶々型と円形型の2つのフェルミ面が存在し、そのどちらも分裂が観測されました。これらの分裂は、過去に報告された同じ試料で行われた角度分解光電子分光測定では見えず、今回の超高分解能測定で初めて観測されたものです。

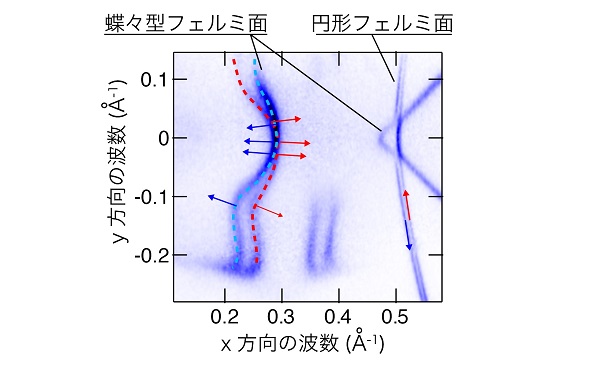
2つのフェルミ面のうち、円形フェルミ面でのスピンの向きは面に対して平行で運動量に対して垂直方向を向いており、ラシュバ効果によって生じるスピンと同じ振る舞いです。それに対し、蝶々型フェルミ面のスピンは表面に平行で運動量に対しても平行方向を向いています。このような蝶々型フェルミ面のスピンの向きは、上述の理想的なラシュバ効果ではもちろん説明できません。

スピンは「電子の円運動」によって誘起される

電子が原子核の周りを円運動すると、「右ネジの法則」のように軌道角運動量によって円軌道の中心を貫く方向に磁場が発現します。

電子スピンは磁場と平行方向か反平行を向くため、このような軌道角運動量によるスピンは円軌道面に垂直方向を向くことになります。また、スピンが磁場と平行か反平行かによってエネルギー差が生じることから、この磁場により縮退している電子バンドはラシュバ効果と同様にスピン分裂することができます。

そこで、2つのフェルミ面の電子軌道を求めたところ、上図の円形フェルミ面では軌道が主に1層目のインジウム原子の周りでxz面上で円運動し、蝶々型フェルミ面では2層目のインジウム原子の周りでyz面上で円運動することがわかりました。xz面上での円運動はy方向のスピンを誘起し、yz面上での円運動はx方向でのスピンを誘起することから、今回の測定で観測された2つのフェルミ面のスピンがどちらも「軌道角運動量」で説明できることがわかりました。

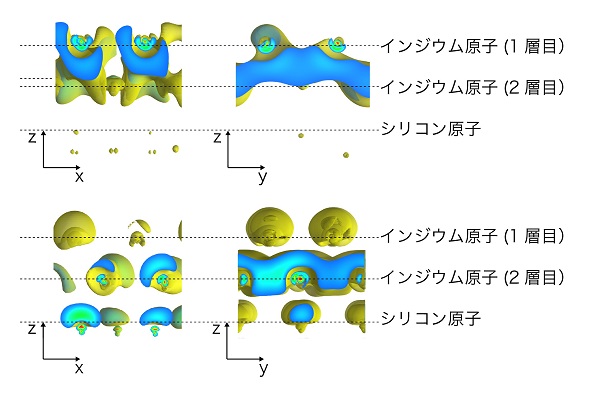
この結果は、これまでラシュバ効果を元に考えられていた原子層結晶などの電子スピンが、電子の運動だけで説明できることを意味しています。つまり、反転対称性の破れた系において、異なる方向を向く電子スピンは電子の運動する軌道を用いて普遍的に説明できることがわかりました。ちなみに、反転対称性が破れていない系では、同じ軌道を反対向きに運動する電子が存在するため、電子スピンは誘起されません。

今後の展望

本研究成果により明らかになった電子の軌道運動に起因した電子スピンの向きは、原子層結晶における電子スピンの動きを理解するためのまったく新しい機構の提唱という学術的意義があるだけでなく、電子スピンを用いた新奇スピントロニクスデバイスの実現に不可欠なものでもあります。

また、本研究で用いたインジウム2層からなる原子層結晶は超伝導となることから、電子スピンを有するトポロジカル超伝導体や新奇超伝導体となる可能性を秘めており、ドーピングなどによってフェルミ面のエネルギーをチューニングすることができれば、応用的にも次世代デバイスとして有力視されているものの未だ商品化されていない量子デバイスの実現を大きく前進させるという意義も併せ持っています。

参考文献
Takahiro Kobayashi, Yoshitaka Nakata, Koichiro Yaji, Tatsuya Shishidou, Daniel Agterberg, Shunsuke Yoshizawa, Fumio Komori, Shik Shin, Michael Weinert, Takashi Uchihashi, and Kazuyuki Sakamoto “Orbital angular momentum induced spin polarization of 2D metallic bands” Phys. Rev. Lett. 125, 176401 (2020).
DOI: https://doi.org/10.1103/PhysRevLett.125.176401